The Pitchfork Bifurcation

In this section we compute a bifurcation diagram for a family of one-dimensional differential equations. In particular, we compute the location of equilibria for a one-parameter family, and compute the saddle-node bifurcations for this family.

Start a new session of Pisces, and open the Model Panel, the Predictor-Corrector Control Panel, and the View Window.

Setting up the Model

Select the DS Pitchfork model from the Model menu on the Main Panel.

We will study the three-parameter family of vector fields on the line given by
x^3 - mu x + alpha + beta mu
as the parameters mu, alpha and beta are varied.

Computing a Locus of Equilibria

We wil compute the locus of equilibria for this vector field in (x,mu)-space. To begin, we must tell Pisces to compute equilibria and also to inflate the domain by the parameter mu.

Create a Derived Model

Select Derived Model from the Settings menu on the Main Panel. The Derived Models Panel will appear. On this panel, select the menu item labeled Fixed Points ODE, then press the Update button that appears.

Inflate the Model Domain

At the bottom of the Model Panel, press the Permute button to bring up the Permutation Panel. Use the Permutation Panel to add the variable mu to the domain. Press the OK button in order to apply the permutation.

Compute the Zero Set of the Derived Model

Change the following parameters on the Predictor-Corrector Control Panel:

Uniform_Points = 0
Boundary_Points = 3
Turning_Points = 3
Singular_Points = 1

Now press Predictor-Corrector's Go button. Change the Hor and Ver coordinates of the View Window in order to project the solution curve onto (mu,x)-space. This curve should look like the pitchfork below (though colors may be different).

For mu<0, the vector field has only one (unstable) equilibria; for mu>0, there are three equilibria (two unstable; one stable).

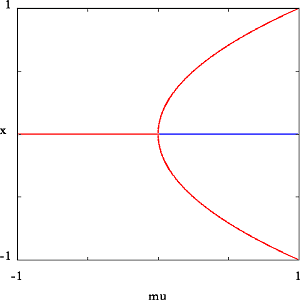
A Locus of Equilibria.

One-Parameter Animation of a Bifurcation Diagram

If the parameter beta is nonzero, the x -> (-x) symmetry in this problem is broken. This symmetry-breaking bifurcation is discussed in Chapter 1 of M. Golubitsky and D. Schaeffer, Singularities and Groups in Bifurcation Theory, I, Springer, 1985.

To view the symmetry-breaking bifurcation, first make sure that the Predictor-Corrector parameters are set as indicated above. Open the Animation Panel by selecting Animate from the Utilities menu of the Main Panel. Animate the parameter Model.beta in eleven (11) steps within the interval [-0.3, 0.3], using the Predcorr algorithm.

What you will see is a pair of nonsingular curves transform into a singular (symmetric) curve and then back into nonsingular curves.

Computing Saddle-Node Bifurcations

We will compute a curve in (x,mu, beta)-space corresponding to saddle-node bifurcations. Geometrically, these are points on the curves of equilibria for which the curve is turning with respect to the parameter mu.

As in the previous problem:

Create a Derived Model: On the Derived Models Panel, select the menu item labeled Saddle Node ODE, then press the Update button that appears.
Inflate the Model Domain: At the bottom of the Model Panel, press the Permute button and use the Permutation Panel to add the variable beta to the domain. Press the OK button to apply the permutation.
Compute the Zero Set of the Derived Model: Press the Go button in the Predictor Corrector Control Panel. Change the Hor and Ver coordinates of the View Window in order to project the saddle-node curve onto (mu,beta)-space. The saddle-node curve separates the parameter space into four regions. A saddle-node bifurcation occurs for parameter values on the curve.
If Geomview is installed on your system, you can view the saddle-node curve in (x,mu,beta)-space. Launch Geomview by selecting the Geomview item from the Output menu. When Geomview appears, it should show a three-dimensional image of the saddle-node curve. If it does not, press the Close button on the Main Panel and then reopen the connection via Output->Geomview in order to force Pisces to resend its current graphics buffer.

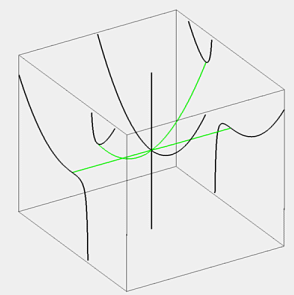
A Saddle Node curve in (x,beta,mu)-space. Three curves of equilibria for fixed beta are included to show that the saddle-node curve corresponds to turning points of the curve of equilibria.

Ending the Session

When you are finished, end this Pisces session by selecting Quit from the File menu on the Main Panel.

The Pisces Home Page