

Next: Complex and Shape
Up: Alpha Shapes: Definition and
Previous: Note...
The 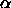 -shape of a finite point set S is a polytope that is uniquely
determined by S and a parameter
-shape of a finite point set S is a polytope that is uniquely
determined by S and a parameter 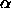 .
It expresses the intuitive notion of the ``shape'' of S,
and
.
It expresses the intuitive notion of the ``shape'' of S,
and 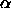 controls the level of detail
reflected by the polytope.
The original paper on
controls the level of detail
reflected by the polytope.
The original paper on 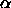 -shapes [6]
defines the concept in
-shapes [6]
defines the concept in 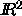 .
An extension to
.
An extension to 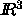 together with
an implementation is reported in [8].
In both papers the relationship between
together with
an implementation is reported in [8].
In both papers the relationship between 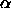 -shapes and
Delaunay triangulations [1]
is described in detail and
used as the basis of an algorithm for constructing alpha shapes.
-shapes and
Delaunay triangulations [1]
is described in detail and
used as the basis of an algorithm for constructing alpha shapes.
These algorithms have been implemented and software for 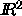 and
and
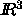 , complete with graphics interface, is publically available.
The respective packages
can be obtained via ftp from:
, complete with graphics interface, is publically available.
The respective packages
can be obtained via ftp from:
ftp://ftp.ncsa.uiuc.edu/Visualization/Alpha-shape/
The availability of these implementations, in particular the one in 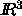 ,
has led to applications in various areas of science and engineering.
Some of these applications are briefly described in [8].
,
has led to applications in various areas of science and engineering.
Some of these applications are briefly described in [8].
A question that was repeatedly asked in the past is
whether it is possible to construct a shape that represents different
levels of detail in different parts of space.
This is indeed possible by assigning a weight to each point.
Intuitively, a large weight favors and a small weight
discourages connections to neighboring points.
We refer to the resulting concept as the weighted alpha shape.
If all weights are zero,
it is the same as the original, unweighted alpha shape.
The available software is general enough to handle weights, and
this document makes no distinction between weighted and
unweighted alpha shapes, unless such a distinction is important.
What are the applications where weights can be beneficial?
- (i)
-
A common computational task in biology is modeling molecular structures.
It is natural to use
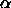 -shapes for this purpose
as they are precise duals of the popular sphere models obtained
by taking unions of balls, see e.g. [13].
The weights are the radii (e.g. van der Waals radii)
of the atoms.
-shapes for this purpose
as they are precise duals of the popular sphere models obtained
by taking unions of balls, see e.g. [13].
The weights are the radii (e.g. van der Waals radii)
of the atoms.
- (ii)
-
In reconstructing a surface from scattered point data,
it is rarely the case that the points are uniformly dense
everywhere on the (unknown) surface.
Indeed, the density often varies with the curvature.
The assignment of large weights in sparse regions and of small weights
in dense regions can be used to counteract the effects resulting
from uneven density distributions.
- (iii)
-
Another goal that can be achieved by assigning weights
is to enforce certain edges or faces.
These might be given as part of the input, but they cannot be
processed directly since alpha shapes are defined only for
finite point sets and not for other geometric objects.
Outline.
Section 2 introduces complexes and shapes via
Voronoi decompositions of spherical ball unions.
Section 3 defines alpha shapes and their relationship to
the (weighted) Delaunay triangulation.
Section 4 discusses metric, combinatorial, and topological
properties computed by the software.
Section 5 reviews some of the essential design
decisions in the implementations.


Next: Complex and Shape
Up: Alpha Shapes: Definition and
Previous: Note...
<epm@ansys.com> 11-Sep-95
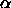 -shape of a finite point set S is a polytope that is uniquely
determined by S and a parameter
-shape of a finite point set S is a polytope that is uniquely
determined by S and a parameter 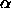 .
It expresses the intuitive notion of the ``shape'' of S,
and
.
It expresses the intuitive notion of the ``shape'' of S,
and 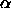 controls the level of detail
reflected by the polytope.
The original paper on
controls the level of detail
reflected by the polytope.
The original paper on 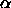 -shapes [6]
defines the concept in
-shapes [6]
defines the concept in 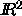 .
An extension to
.
An extension to 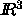 together with
an implementation is reported in [8].
In both papers the relationship between
together with
an implementation is reported in [8].
In both papers the relationship between 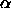 -shapes and
Delaunay triangulations [1]
is described in detail and
used as the basis of an algorithm for constructing alpha shapes.
-shapes and
Delaunay triangulations [1]
is described in detail and
used as the basis of an algorithm for constructing alpha shapes.
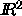 and
and
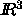 , complete with graphics interface, is publically available.
The respective packages
can be obtained via ftp from:
, complete with graphics interface, is publically available.
The respective packages
can be obtained via ftp from:
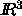 ,
has led to applications in various areas of science and engineering.
Some of these applications are briefly described in [
,
has led to applications in various areas of science and engineering.
Some of these applications are briefly described in [ -shapes for this purpose
as they are precise duals of the popular sphere models obtained
by taking unions of balls, see e.g. [13].
The weights are the radii (e.g. van der Waals radii)
of the atoms.
-shapes for this purpose
as they are precise duals of the popular sphere models obtained
by taking unions of balls, see e.g. [13].
The weights are the radii (e.g. van der Waals radii)
of the atoms.