

Next: References
Up: Alpha Shapes: Definition and
Previous: Signatures
The main two data structures built and used by our software
are the Delaunay simplicial complex, 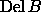 ,
and a filter whose filtration contains all alpha complexes.
The filter is accessible through a linear list and an interval tree.
The list supports the computation of signatures,
and the tree provides fast access to individual shapes.
We restrict the discussion to d = 3 dimensions.
,
and a filter whose filtration contains all alpha complexes.
The filter is accessible through a linear list and an interval tree.
The list supports the computation of signatures,
and the tree provides fast access to individual shapes.
We restrict the discussion to d = 3 dimensions.
In 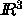 ,
, 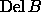 is represented by a
triangle-based pointer structure [3].
Each triangle is stored with a pointer each to the 6 neighboring
triangles sharing an edge.
Following appropriate pointers, each in constant time,
it is possible to traverse the triangles around a given edge,
or the triangles opposite a given vertex,
or all triangles on the convex hull boundary.
Further details can be found in [12].
is represented by a
triangle-based pointer structure [3].
Each triangle is stored with a pointer each to the 6 neighboring
triangles sharing an edge.
Following appropriate pointers, each in constant time,
it is possible to traverse the triangles around a given edge,
or the triangles opposite a given vertex,
or all triangles on the convex hull boundary.
Further details can be found in [12].
An important ingredient in the construction of 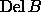 ,
which is synonymous to constructing its triangle-based pointer
structure,
is the use of exact arithmetic and symbolic computation.
The input coordinates and weights are restricted to integers
or fixed-point reals.
(A negative weight, -w, is interpreted as
,
which is synonymous to constructing its triangle-based pointer
structure,
is the use of exact arithmetic and symbolic computation.
The input coordinates and weights are restricted to integers
or fixed-point reals.
(A negative weight, -w, is interpreted as 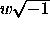 .)
All geometric tests are performed in exact arithmetic so that
degenerate cases can be identified without ambiguity.
Such degeneracies include 4 points on a common plane, and
5 balls with common orthogonal sphere.
All possible degeneracies are reduced to the general case by the
use of a simulated perturbation [7].
In the presence of coplanar point on the convex hull boundary,
the perturbation results in the construction of infinitesimally thin
tetrahedra.
As a fortunate consequence of the perturbation scheme in [7]
no infinitesimally thin tetrahedra can occur in the
interior of the convex hull.
The artifacts at the boundary are removed in a post-processing step.
.)
All geometric tests are performed in exact arithmetic so that
degenerate cases can be identified without ambiguity.
Such degeneracies include 4 points on a common plane, and
5 balls with common orthogonal sphere.
All possible degeneracies are reduced to the general case by the
use of a simulated perturbation [7].
In the presence of coplanar point on the convex hull boundary,
the perturbation results in the construction of infinitesimally thin
tetrahedra.
As a fortunate consequence of the perturbation scheme in [7]
no infinitesimally thin tetrahedra can occur in the
interior of the convex hull.
The artifacts at the boundary are removed in a post-processing step.
The linear list representation of the filter contains slightly
more information than just the sequence of simplices as they enter
the alpha complex.
Each simplex occurs up to three times:
first when it enters the alpha complex,
second when the first simplex containing it as a face enters the
alpha complex,
and third when it becomes completely surrounded by simplices.
After the first occurrence the simplex is singular,
after the second it is regular,
and after the third it is interior.
Quite commonly some of the occurrences coincide or vanish.
For example, a simplex on the convex hull boundary is never interior,
and an entering tetrahedron is right away considered interior.
The additional information available through the multiple occurrences
is e.g. useful in selecting the simplices needed for a
graphical representation.
Only the boundary triangles (singular and regular),
the singular edges, and the singular vertices need to be displayed.
A triangle belongs to the boundary of all shapes between its first
and its third occurrence.
Each triangle thus gives rise to an interval of indices in the
filtration, and given an index, the corresponding shape is drawn by
recovering all triangles whose intervals cover the index.
These triangles are located using the interval tree [4]
storing their intervals.
Except for an additive logarithmic overhead term,
it enumerates the desired triangles in constant time each.
The same mechanism applies to singular edges and vertices.


Next: References
Up: Alpha Shapes: Definition and
Previous: Signatures
<epm@ansys.com> 11-Sep-95
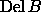 ,
and a filter whose filtration contains all alpha complexes.
The filter is accessible through a linear list and an interval tree.
The list supports the computation of signatures,
and the tree provides fast access to individual shapes.
We restrict the discussion to d = 3 dimensions.
,
and a filter whose filtration contains all alpha complexes.
The filter is accessible through a linear list and an interval tree.
The list supports the computation of signatures,
and the tree provides fast access to individual shapes.
We restrict the discussion to d = 3 dimensions.
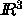 ,
, 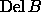 is represented by a
triangle-based pointer structure [
is represented by a
triangle-based pointer structure [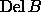 ,
which is synonymous to constructing its triangle-based pointer
structure,
is the use of exact arithmetic and symbolic computation.
The input coordinates and weights are restricted to integers
or fixed-point reals.
(A negative weight, -w, is interpreted as
,
which is synonymous to constructing its triangle-based pointer
structure,
is the use of exact arithmetic and symbolic computation.
The input coordinates and weights are restricted to integers
or fixed-point reals.
(A negative weight, -w, is interpreted as 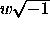 .)
All geometric tests are performed in exact arithmetic so that
degenerate cases can be identified without ambiguity.
Such degeneracies include 4 points on a common plane, and
5 balls with common orthogonal sphere.
All possible degeneracies are reduced to the general case by the
use of a simulated perturbation [
.)
All geometric tests are performed in exact arithmetic so that
degenerate cases can be identified without ambiguity.
Such degeneracies include 4 points on a common plane, and
5 balls with common orthogonal sphere.
All possible degeneracies are reduced to the general case by the
use of a simulated perturbation [