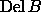 implicitly represents all alpha
complexes defined by B as prefixes.
The availability of this simplex sequence favors
incremental algorithms for computing properties of alpha shapes.
The software considers metric properties:
implicitly represents all alpha
complexes defined by B as prefixes.
The availability of this simplex sequence favors
incremental algorithms for computing properties of alpha shapes.
The software considers metric properties:
The filter of 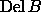 implicitly represents all alpha
complexes defined by B as prefixes.
The availability of this simplex sequence favors
incremental algorithms for computing properties of alpha shapes.
The software considers metric properties:
implicitly represents all alpha
complexes defined by B as prefixes.
The availability of this simplex sequence favors
incremental algorithms for computing properties of alpha shapes.
The software considers metric properties:
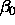 ,
,
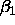 ,
,
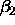 .
.
As shown in [11],
every additive and continuous map from
the set of convex bodies to 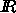 invariant under rigid motion
is a linear combination of quermassintegrals,
see also [14, chapter 4,].
In
invariant under rigid motion
is a linear combination of quermassintegrals,
see also [14, chapter 4,].
In 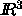 , the quermassintegrals are basically
volume, area, mean width, and the Euler number.
Length is defined as an extension of the mean width
to non-convex bodies.
Specifically, length is the sum of edge lengths, each
weighted by the (possibly negative) complementary angle.
The Euler number is
, the quermassintegrals are basically
volume, area, mean width, and the Euler number.
Length is defined as an extension of the mean width
to non-convex bodies.
Specifically, length is the sum of edge lengths, each
weighted by the (possibly negative) complementary angle.
The Euler number is 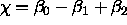 .
.
Each property defines a signature
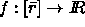 ,
where
,
where 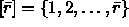 .
Signatures are useful in studying shapes and convenient in
quickly identifying the ``interesting'' ones in the typically huge
family of alpha shapes.
.
Signatures are useful in studying shapes and convenient in
quickly identifying the ``interesting'' ones in the typically huge
family of alpha shapes.
The signatures expressing the above metric and combinatorial properties are straightforward to compute: scan the filter from 0 through n and increment or decrement the current value depending on the next simplex. Such a strategy also works for the three betti numbers, but is less obvious [2].