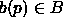 simultaneously without changing Voronoi cells.
In this case, all cells of the decomposition C of
simultaneously without changing Voronoi cells.
In this case, all cells of the decomposition C of
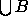 can only
grow, and the dual complex can only get larger.
The result is a one-parametric family of simplicial complexes.
can only
grow, and the dual complex can only get larger.
The result is a one-parametric family of simplicial complexes.
Suppose we grow all balls
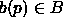 simultaneously without changing Voronoi cells.
In this case, all cells of the decomposition C of
simultaneously without changing Voronoi cells.
In this case, all cells of the decomposition C of
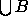 can only
grow, and the dual complex can only get larger.
The result is a one-parametric family of simplicial complexes.
can only
grow, and the dual complex can only get larger.
The result is a one-parametric family of simplicial complexes.
More formally, let 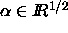 ,
,
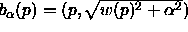 ,
and
,
and
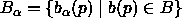 .
For
.
For 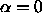 the radius of
the radius of
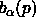 is its weight,
and for
is its weight,
and for 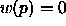 the radius is
the radius is
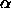 .
By construction, the Voronoi cell of
.
By construction, the Voronoi cell of 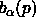 in
in 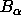 is the same as the Voronoi cell of
is the same as the Voronoi cell of 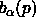 in B.
The
in B.
The 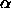 -complex,
-complex,
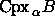 ,
is the dual complex of
,
is the dual complex of 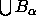 .
The
.
The 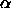 -shape is
-shape is
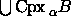 .
By monotonicity of the cells
.
By monotonicity of the cells
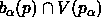 ,
we have
,
we have

whenever 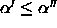 .
For sufficiently large
.
For sufficiently large 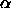 ,
,
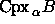 geometrically
realizes the nerve of the collection of Voronoi cells.
We refer to this complex as the
(weighted) Delaunay simplicial complex or
(weighted) Delaunay triangulation of B,
and denote this by
geometrically
realizes the nerve of the collection of Voronoi cells.
We refer to this complex as the
(weighted) Delaunay simplicial complex or
(weighted) Delaunay triangulation of B,
and denote this by 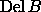 .
All
.
All 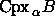 are subcomplexes of
are subcomplexes of 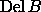 .
.
Since 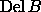 is a finite complex,
there are only finitely many subcomplexes,
and the ones we are interested in are naturally ordered by inclusion.
We index the complexes from 0 through
is a finite complex,
there are only finitely many subcomplexes,
and the ones we are interested in are naturally ordered by inclusion.
We index the complexes from 0 through 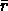 , and
define
, and
define 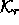 as the r-th complex after the trivial complex,
as the r-th complex after the trivial complex,
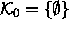 .
The last complex is
.
The last complex is 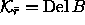 .
.
The linear structure is essential in obtaining algorithms that
efficiently deal with the entire family of alpha complexes and shapes.
As a consequence, the most important step in the computation
is the construction of 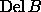 .
Many efficient algorithms
have been described in the literature.
The implementation provided as part of our software distribution builds
.
Many efficient algorithms
have been described in the literature.
The implementation provided as part of our software distribution builds
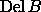 incrementally, adding each point by a sequence of flips
[9].
The points are added in random order.
incrementally, adding each point by a sequence of flips
[9].
The points are added in random order.
The linear sequence of alpha complexes can be understood as assembling
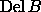 one simplex at a time.
This is not quite correct because
one simplex at a time.
This is not quite correct because 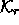 and
and 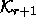 may differ
by more than only one simplex.
In such a case, we can add the simplices in
may differ
by more than only one simplex.
In such a case, we can add the simplices in 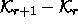 one by one, lower dimensions first.
The resulting sequence of simplices,
one by one, lower dimensions first.
The resulting sequence of simplices,

is called a filter, and the sequence of complexes,
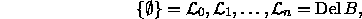
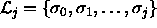 ,
is a filtration.
For each
,
is a filtration.
For each 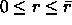 , t
here is a
, t
here is a 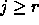 and an
and an 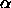 with
with 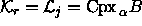 .
.