

Next: Filter and Filtration
Up: Alpha Shapes: Definition and
Previous: Introduction
Up front two remarks to avoid any confusion and misconceptions.
First, it is more cumbersome to distinguish between d=2 and d=3
dimensions than to phrase all definitions in 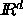 ,
for some arbitrary but fixed positive integer d.
Second, we use square roots of real numbers as weights.
Since negative weight squares do make sense,
we choose
,
for some arbitrary but fixed positive integer d.
Second, we use square roots of real numbers as weights.
Since negative weight squares do make sense,
we choose 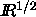 as the domain for all point weights.
This is the set of all (positive) square roots of
real numbers, and it inherits its linear order from
as the domain for all point weights.
This is the set of all (positive) square roots of
real numbers, and it inherits its linear order from 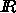 .
.
A point 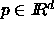 with weight
with weight 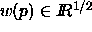 ,
is interpreted as a spherical ball,
,
is interpreted as a spherical ball,
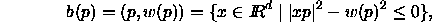
with center p and
radius 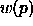 ,
where |yz| denotes the Euclidean distance between points y and z.
All points with non-real weight correspond to empty balls.
,
where |yz| denotes the Euclidean distance between points y and z.
All points with non-real weight correspond to empty balls.
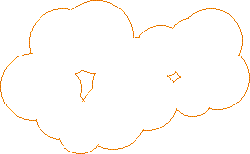
Figure 1: The union of a set of disks in the plane.
The shape of a finite set 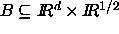 of weighted points is defined in terms of a decomposition of
the union of balls,
of weighted points is defined in terms of a decomposition of
the union of balls, 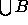 , into convex sets
(see, for example, figures 1 and 2).
, into convex sets
(see, for example, figures 1 and 2).
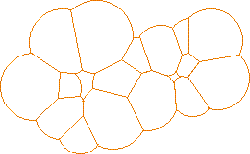
Figure 2: The decomposition of the union of disks defind by their
Voronoi cells.
The (weighted) Voronoi cell of a ball 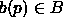 is
is
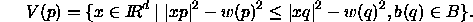
It is a convex polyhedron, and its intersection with the ball union
is convex because
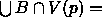
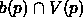 .
Note that the convex cells have pairwise disjoint interiors,
but some of them overlap along common boundary pieces.
These pieces of overlap are instrumental in the construction
of a set system closed under the subset operation.
In topology, such a system is referred to as an
abstract simplicial complex.
Specifically, we define the nerve of
.
Note that the convex cells have pairwise disjoint interiors,
but some of them overlap along common boundary pieces.
These pieces of overlap are instrumental in the construction
of a set system closed under the subset operation.
In topology, such a system is referred to as an
abstract simplicial complex.
Specifically, we define the nerve of
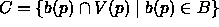 as
as
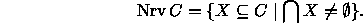
Assuming general position of the points or balls, the largest
set in 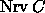 is
of size d+1, i.e.,
a triple in
is
of size d+1, i.e.,
a triple in  and
a quadruple in
and
a quadruple in 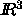 .
Under this assumption,
.
Under this assumption, 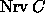 has a natural geometric realization
by mapping each cell
has a natural geometric realization
by mapping each cell 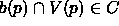 to the point
to the point
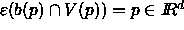 .
This realization is a (geometric) simplicial complex,
.
This realization is a (geometric) simplicial complex, 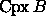 ,
see e.g. [10].
Each set
,
see e.g. [10].
Each set 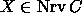 is represented by the convex hull of the
corresponding points:
the points are the images of the cells in X and their convex
hull is a simplex of dimension one less than the cardinality of X.
Formally,
is represented by the convex hull of the
corresponding points:
the points are the images of the cells in X and their convex
hull is a simplex of dimension one less than the cardinality of X.
Formally,
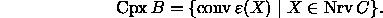

Figure 3: The dual complex of the disk union.
We refer to this complex as the dual complex of 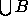 ,
and to its underlying space,
,
and to its underlying space,
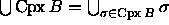 ,
as the dual shape (see figures 3 and 4).
,
as the dual shape (see figures 3 and 4).
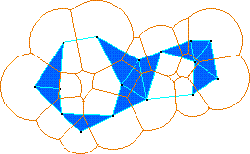
Figure: The decomposition of the union of disks and its dual complex
(figures 2 and 3 overlapped).
Among the most useful properties of 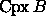 are the homotopy
equivalence between
are the homotopy
equivalence between
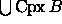 and
and
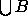 , and the
fact
, and the
fact 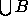 can be expressed as the alternating sum of common
ball intersections, with one term per simplex in
can be expressed as the alternating sum of common
ball intersections, with one term per simplex in 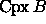 .
This implies short inclusion-exclusion formulas for the
d-dimensional volume and other measures of
.
This implies short inclusion-exclusion formulas for the
d-dimensional volume and other measures of
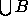 ,
see [5].
,
see [5].


Next: Filter and Filtration
Up: Alpha Shapes: Definition and
Previous: Introduction
<epm@ansys.com> 11-Sep-95
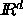 ,
for some arbitrary but fixed positive integer d.
Second, we use square roots of real numbers as weights.
Since negative weight squares do make sense,
we choose
,
for some arbitrary but fixed positive integer d.
Second, we use square roots of real numbers as weights.
Since negative weight squares do make sense,
we choose 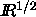 as the domain for all point weights.
This is the set of all (positive) square roots of
real numbers, and it inherits its linear order from
as the domain for all point weights.
This is the set of all (positive) square roots of
real numbers, and it inherits its linear order from 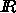 .
.
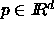 with weight
with weight 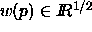 ,
is interpreted as a spherical ball,
,
is interpreted as a spherical ball,
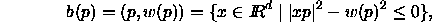
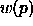 ,
where |yz| denotes the Euclidean distance between points y and z.
All points with non-real weight correspond to empty balls.
,
where |yz| denotes the Euclidean distance between points y and z.
All points with non-real weight correspond to empty balls.

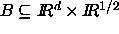 of weighted points is defined in terms of a decomposition of
the union of balls,
of weighted points is defined in terms of a decomposition of
the union of balls, 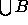 , into convex sets
(see, for example, figures
, into convex sets
(see, for example, figures 
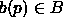 is
is
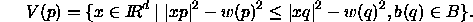
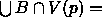
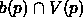 .
Note that the convex cells have pairwise disjoint interiors,
but some of them overlap along common boundary pieces.
These pieces of overlap are instrumental in the construction
of a set system closed under the subset operation.
In topology, such a system is referred to as an
abstract simplicial complex.
Specifically, we define the nerve of
.
Note that the convex cells have pairwise disjoint interiors,
but some of them overlap along common boundary pieces.
These pieces of overlap are instrumental in the construction
of a set system closed under the subset operation.
In topology, such a system is referred to as an
abstract simplicial complex.
Specifically, we define the nerve of
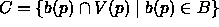 as
as
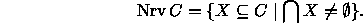
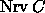 is
of size d+1, i.e.,
a triple in
is
of size d+1, i.e.,
a triple in 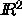 and
a quadruple in
and
a quadruple in 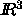 .
Under this assumption,
.
Under this assumption, 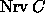 has a natural geometric realization
by mapping each cell
has a natural geometric realization
by mapping each cell 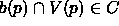 to the point
to the point
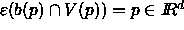 .
This realization is a (geometric) simplicial complex,
.
This realization is a (geometric) simplicial complex, 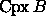 ,
see e.g. [
,
see e.g. [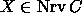 is represented by the convex hull of the
corresponding points:
the points are the images of the cells in X and their convex
hull is a simplex of dimension one less than the cardinality of X.
Formally,
is represented by the convex hull of the
corresponding points:
the points are the images of the cells in X and their convex
hull is a simplex of dimension one less than the cardinality of X.
Formally,
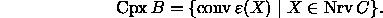

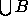 ,
and to its underlying space,
,
and to its underlying space,
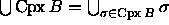 ,
as the dual shape (see figures
,
as the dual shape (see figures 
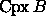 are the homotopy
equivalence between
are the homotopy
equivalence between
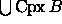 and
and
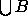 , and the
fact
, and the
fact 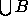 can be expressed as the alternating sum of common
ball intersections, with one term per simplex in
can be expressed as the alternating sum of common
ball intersections, with one term per simplex in 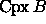 .
This implies short inclusion-exclusion formulas for the
d-dimensional volume and other measures of
.
This implies short inclusion-exclusion formulas for the
d-dimensional volume and other measures of
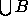 ,
see [
,
see [