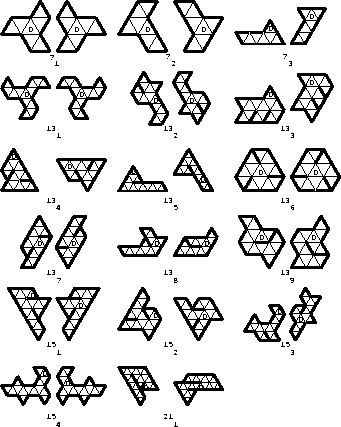
Figure 4: Isospectral domains.
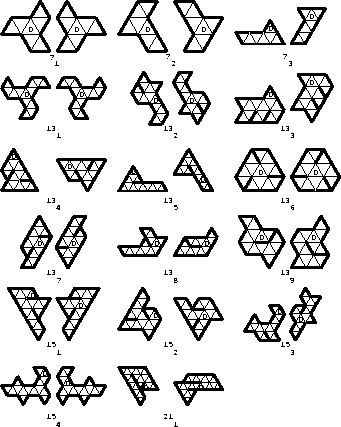
Figure 4: Isospectral domains.
Figure 4 shows pairs of diagrams representing domains whose isospectrality can be verified using the method of transplantation. Each pair of diagrams represents not a single pair of isospectral domains, but a whole family of pairs of isospectral domains, gotten by replacing the equilateral triangles with general triangles so that the triangles labelled 0 are mapped onto one another by a translation and the remaining triangles are obtained from these by the appropriate sequence of reflections. We have seen two examples of this already, in Figures 3 and 1. Further examples generated in this way are shown in Section 5.
The pair 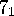 is the pair of propeller diagrams discussed in detail above.
The pair
is the pair of propeller diagrams discussed in detail above.
The pair 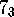 yields a simplified version of the
pair of isospectral domains
given by Gordon, Webb, and Wolpert
[5],
[4],
which was obtained by bisecting a pair of flat but non-planar isospectral
domains given earlier by Buser
[2].
The pair
yields a simplified version of the
pair of isospectral domains
given by Gordon, Webb, and Wolpert
[5],
[4],
which was obtained by bisecting a pair of flat but non-planar isospectral
domains given earlier by Buser
[2].
The pair 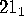 yields the homophonic domains
shown in Figure 1 above.
In this case we must be careful to choose the relevant
angle of our generating triangle to be
yields the homophonic domains
shown in Figure 1 above.
In this case we must be careful to choose the relevant
angle of our generating triangle to be 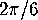 since six of these angles
meet around a vertex in each domain.
If we do not choose the angle to be
since six of these angles
meet around a vertex in each domain.
If we do not choose the angle to be 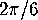 ,
then instead of planar domains
we get a pair of isospectral cone-manifolds.
,
then instead of planar domains
we get a pair of isospectral cone-manifolds.
Note that in order for the pair 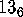 to yield a pair
of non-overlapping non-congruent domains
we must decrease all three angles simultaneously, which we can
do by using hyperbolic triangles in place of Euclidean
triangles. Using hyperbolic triangles, we can easily produce isospectral
pairs of convex domains in the hyperbolic plane, but we do not
know of any such pairs in the Euclidean plane.
to yield a pair
of non-overlapping non-congruent domains
we must decrease all three angles simultaneously, which we can
do by using hyperbolic triangles in place of Euclidean
triangles. Using hyperbolic triangles, we can easily produce isospectral
pairs of convex domains in the hyperbolic plane, but we do not
know of any such pairs in the Euclidean plane.