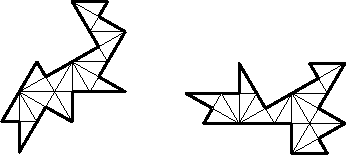
Figure 1: Homophonic domains. These drums sound the same when struck at the interior points where six triangles meet.
In 1965, Mark Kac [6] asked, `Can one hear the shape of a drum?', so popularizing the question of whether there can exist two non-congruent isospectral domains in the plane. In the ensuing 25 years many examples of isospectral manifolds were found, whose dimensions, topology, and curvature properties gradually approached those of the plane. Recently, Gordon, Webb, and Wolpert [5] finally reduced the examples into the plane. In this note, we give a number of examples, and a particularly simple method of proof. One of our examples (see Figure 1) is a pair of domains that are not only isospectral but homophonic: Each domain has a distinguished point such that corresponding normalized Dirichlet eigenfunctions take equal values at the distinguished points. We interpret this to mean that if the corresponding `drums' are struck at these special points, then they `sound the same' in the very strong sense that every frequency will be excited to the same intensity for each. This shows that one really can't hear the shape of a drum.
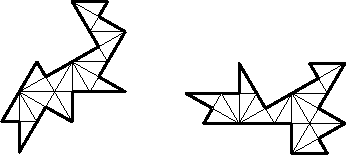
Figure 1: Homophonic domains. These drums sound the
same when struck at the interior points
where six triangles meet.