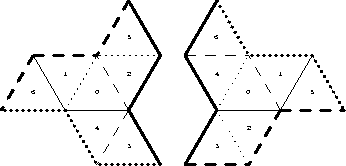
Figure 2: Propeller example.
The following transplantation proof was first applied to Riemann surfaces by Buser [1]. For our domains this proof turns out to be particularly easy.
Consider the two propeller-shaped regions shown in Figure 2. Each region consists of seven equilateral triangles (labelled in some unspecified way). Our first pair of examples is obtained from these by replacing the equilateral triangles by acute-angled scalene triangles, all congruent to each other. The propellers are triangulated by these triangles in such a way that any two triangles that meet along a line are mirror images in that line, as in Figure 3. In both propellers the central triangle has a distinguishing property: its sides connect the three inward corners of the propeller. The position of the propellers in Figure 3 is such that the unique isometry from the central triangle on the left-hand side to the central triangle on the right-hand side is a translation. This translation does not map the propellers onto one another and so they are not isometric.
Now let 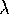 be any real number, and
be any real number, and 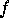 any
eigenfunction of the
Laplacian with eigenvalue
any
eigenfunction of the
Laplacian with eigenvalue 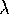 for the Dirichlet problem
corresponding
to the left-hand propeller.
Let
for the Dirichlet problem
corresponding
to the left-hand propeller.
Let 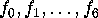 denote the functions obtained
by restricting
denote the functions obtained
by restricting 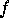 to each of the 7 triangles of the left-hand
propeller,
as indicated on the left in Figure 3.
For brevity, we write
to each of the 7 triangles of the left-hand
propeller,
as indicated on the left in Figure 3.
For brevity, we write 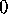 for
for 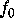 ,
, 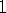 for
for 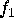 , etc.
The Dirichlet boundary condition is that
, etc.
The Dirichlet boundary condition is that 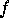 must vanish
on each boundary-segment. Using the reflection principle, this
is equivalent to the assertion that
must vanish
on each boundary-segment. Using the reflection principle, this
is equivalent to the assertion that 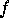 would
go into
would
go into 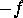 if continued as a smooth eigenfunction across
any boundary-segment. (More precisely it goes into
if continued as a smooth eigenfunction across
any boundary-segment. (More precisely it goes into 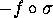 where
where 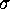 is the reflection on the boundary segment.)
is the reflection on the boundary segment.)
On the right in Figure 3,
we show how to obtain from 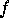 another eigenfunction
of eigenvalue
another eigenfunction
of eigenvalue 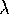 , this time for the right-hand propeller. In
the
central triangle, we put the function
, this time for the right-hand propeller. In
the
central triangle, we put the function 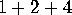 . By this
we mean the function
. By this
we mean the function 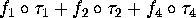 where
for
where
for 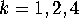 ,
, 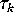 is the isometry from the central triangle
of the right-hand propeller to the triangle labelled
is the isometry from the central triangle
of the right-hand propeller to the triangle labelled 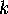 on the
left-hand propeller.
Now we see from the left-hand side that the functions
on the
left-hand propeller.
Now we see from the left-hand side that the functions 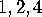 continue smoothly across dotted lines into copies of the
functions
continue smoothly across dotted lines into copies of the
functions 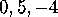 respectively, so that their
sum continues into
respectively, so that their
sum continues into 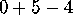 as shown. The reader
should check in a similar way that this continues across a solid
line to
as shown. The reader
should check in a similar way that this continues across a solid
line to 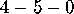 (its negative), and across a dashed line to
(its negative), and across a dashed line to
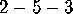 , which continues across either a solid or dotted
line to its own negative. These
assertions, together with the similar ones obtained by symmetry (i.e. cyclic
permutation of the arms of the propellers),
are enough to show that the transplanted function is an eigenfunction
of eigenvalue
, which continues across either a solid or dotted
line to its own negative. These
assertions, together with the similar ones obtained by symmetry (i.e. cyclic
permutation of the arms of the propellers),
are enough to show that the transplanted function is an eigenfunction
of eigenvalue 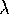 that vanishes along each boundary segment
of the right-hand propeller.
that vanishes along each boundary segment
of the right-hand propeller.
So we have defined a linear map which for each 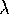 takes the
takes the
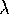 -eigenspace for the left-hand propeller to the
-eigenspace for the left-hand propeller to the
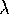 -eigenspace
for the right-hand one. This is easily checked to be a
non-singular map, and so the dimension of the eigenspace
on the right-hand side is larger or equal the dimension
on the left-hand side. Since the same transplantation may also
be applied in the reversed direction the dimensions are equal.
This holds for each
-eigenspace
for the right-hand one. This is easily checked to be a
non-singular map, and so the dimension of the eigenspace
on the right-hand side is larger or equal the dimension
on the left-hand side. Since the same transplantation may also
be applied in the reversed direction the dimensions are equal.
This holds for each 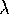 , and so the two propellers are Dirichlet
isospectral.
, and so the two propellers are Dirichlet
isospectral.
In fact they are also Neumann isospectral, as can be seen by a similar transplantation proof obtained by replacing every minus sign in the above by a plus sign. (Going from Neumann to Dirichlet is almost as easy: Just color the triangles on each side alternately black and white, and attach minus signs on the right to function elements that have moved from black to white or vice versa.)
In the propeller example,
each of the seven function elements on the left
got transplanted into three triangles on the right, and we verified
that it all fits together seamlessly.
If we hadn't been given the transplantation rule, we could have worked it
out as follows:
We start by transplanting
the function element 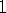 into the central triangle on the right;
on the left
into the central triangle on the right;
on the left 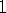 continues across a dotted line to
continues across a dotted line to 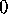 , so we stick
, so we stick 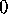 in the triangle across the dotted line on the right; on the left
in the triangle across the dotted line on the right; on the left 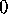 continues across the solid line to
continues across the solid line to 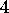 , and since on the right
the solid side of the
triangle containing
, and since on the right
the solid side of the
triangle containing 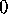 is a boundary edge, we stick a
is a boundary edge, we stick a
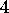 in along with the
in along with the 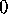 (don't worry about signs-we can fill them in afterwards using the
black and white coloring of the triangles);
now since on the left
(don't worry about signs-we can fill them in afterwards using the
black and white coloring of the triangles);
now since on the left
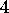 continues across a dotted line to itself
we stick a
continues across a dotted line to itself
we stick a 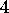 into the center along
with the
into the center along
with the 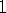 we started with; and so on until we have three function
elements in each triangle on the right and the whole thing fits together
seamlessly.
we started with; and so on until we have three function
elements in each triangle on the right and the whole thing fits together
seamlessly.
If we had begun by putting 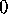 into
the central triangle on the right, rather than
into
the central triangle on the right, rather than 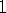 ,
then we would have ended up with four function
elements in each triangle, namely, the complement in the set
,
then we would have ended up with four function
elements in each triangle, namely, the complement in the set
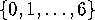 of the original three;
This gives a second transplantation mapping.
Call the original mapping
of the original three;
This gives a second transplantation mapping.
Call the original mapping 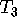 , and the complementary mapping
, and the complementary mapping 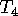 .
Any linear combination
.
Any linear combination 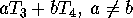 will also be a transplantation mapping,
and if we take for
will also be a transplantation mapping,
and if we take for 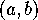 one of the four solutions
to the equations
one of the four solutions
to the equations 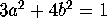 ,
,
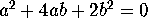 ,
our transplantation mapping
becomes norm-preserving.
,
our transplantation mapping
becomes norm-preserving.
Now consider the
pair of putatively homophonic domains shown in Figure 1 above.
In this case we find two complementary transplantation mappings
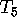 and
and 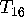 .
The linear combination
.
The linear combination 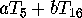 is a norm-preserving
mapping if
is a norm-preserving
mapping if
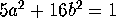 and
and 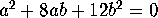 , that is, if
, that is, if
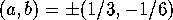 or
or 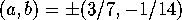 .
In the Dirichlet case, transplantation is kind to the values of the
transplanted functions at the special interior points where six triangles
meet.
With the proper choice of sign,
the Dirichlet incarnation of
.
In the Dirichlet case, transplantation is kind to the values of the
transplanted functions at the special interior points where six triangles
meet.
With the proper choice of sign,
the Dirichlet incarnation of 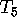 multiplies the special value
by 2,
the Dirichlet incarnation of
multiplies the special value
by 2,
the Dirichlet incarnation of 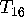 multiplies the special value by
multiplies the special value by
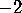 ,
and the four norm-preserving linear combinations
,
and the four norm-preserving linear combinations
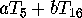 specified above multiply it by
specified above multiply it by
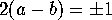 .
Thus we can convert an orthonormal basis of Dirichlet
eigenfunctions on the left to one on the right
so that corresponding functions take on the same special value.
This shows that the two domains are homophonic,
or more specifically, Dirichlet homophonic.
There is no similar reason for these domains to be Neumann homophonic,
and, in fact, we
do not know of any pair of non-congruent Neumann homophonic domains.
.
Thus we can convert an orthonormal basis of Dirichlet
eigenfunctions on the left to one on the right
so that corresponding functions take on the same special value.
This shows that the two domains are homophonic,
or more specifically, Dirichlet homophonic.
There is no similar reason for these domains to be Neumann homophonic,
and, in fact, we
do not know of any pair of non-congruent Neumann homophonic domains.