More about the examples
Next: Special cases of
Up: Some planar isospectral domains
Previous: Gallery of examples
The examples in the previous section were
obtained by applying a theorem of Sunada
[7].
Let 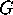 be a finite group.
Call two subgroups
be a finite group.
Call two subgroups 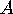 and
and 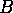 of
of 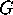 isospectral
if each element of
isospectral
if each element of 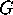 belongs to just as many conjugates of
belongs to just as many conjugates of 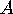 as of
as of 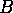 .
(This is equivalent to requiring that
.
(This is equivalent to requiring that 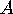 and
and 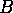 have the same number of elements in each conjugacy class of
have the same number of elements in each conjugacy class of 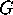 .)
Sunada's theorem states that
if
.)
Sunada's theorem states that
if 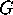 acts on a manifold
acts on a manifold 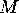 and
and 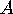 and
and 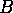 are isospectral subgroups of
are isospectral subgroups of
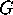 , then the quotient spaces of
, then the quotient spaces of 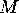 by
by 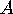 and
and 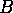 are
isospectral.
are
isospectral.
The tables in this section show for each of the examples a trio of elements
which generate the appropriate 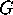 , in two distinct permutation
representations. The isospectral subgroups
, in two distinct permutation
representations. The isospectral subgroups 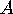 and
and 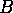 are the
point-stabilizers in these two permutation representations.
are the
point-stabilizers in these two permutation representations.
For the example 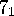 , the details are as follows.
, the details are as follows.
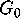 is the group of motions of the hyperbolic plane
generated by the reflections
is the group of motions of the hyperbolic plane
generated by the reflections 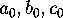 in the sides of
a triangle whose three angles are
in the sides of
a triangle whose three angles are 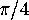 .
In Conway's orbifold notation
(see [3]),
.
In Conway's orbifold notation
(see [3]),
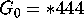 .
.
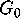 has a homomorphism
has a homomorphism
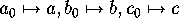 onto the finite group
onto the finite group 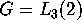 (also known as
(also known as 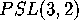 ),
the automorphism group of the projective plane of order 2.
The generators of
),
the automorphism group of the projective plane of order 2.
The generators of 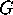 act on the points and lines of this plane
(with respect to some unspecified numbering of the points and lines)
as follows:
act on the points and lines of this plane
(with respect to some unspecified numbering of the points and lines)
as follows:
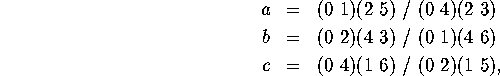
where the actions on points and lines are separated by 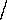 .
.
The group 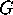 has two subgroups
has two subgroups 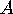 and
and 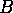 of index 7, namely
the stabilizers of a point or a line. The preimages
of index 7, namely
the stabilizers of a point or a line. The preimages 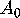 and
and 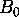 of these two groups in
of these two groups in 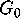 have fundamental regions that consist of
7 copies of the original triangle, glued together as in Figure 2.
Each of these is a hexagon of angles
have fundamental regions that consist of
7 copies of the original triangle, glued together as in Figure 2.
Each of these is a hexagon of angles 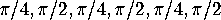 ,
and so
each of
,
and so
each of 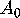 and
and 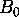 is a copy of the reflection group
is a copy of the reflection group 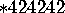 .
.
The preimage in 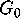 of the trivial subgroup of
of the trivial subgroup of 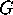 is a group
is a group
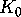 of index 168. The quotient of the hyperbolic plane by
of index 168. The quotient of the hyperbolic plane by 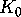 is a 23-fold
cross-surface (that is to say, the connected sum of 23 real projective
planes),
so that in Conway's orbifold notation
is a 23-fold
cross-surface (that is to say, the connected sum of 23 real projective
planes),
so that in Conway's orbifold notation
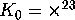 .
Deforming the metric on this 23-fold cross surface by replacing
its hyperbolic triangles by scalene Euclidean triangles yields a
cone-manifold
.
Deforming the metric on this 23-fold cross surface by replacing
its hyperbolic triangles by scalene Euclidean triangles yields a
cone-manifold 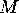 whose quotients by
whose quotients by 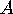 and
and 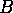 are non-congruent
planar isospectral domains.
are non-congruent
planar isospectral domains.
Tables 1 and 2
display the corresponding information for our other examples.

Table 1: Specifications.

Table 2: Permutations.
Note that the permutations in Table 2 correspond to the neighboring
relations in Figure 4. In the propeller
example, for instance, the pairs 0, 1 and 2, 5
are neighbors along a dotted line
on the left-hand side, and 0, 4 and 2, 3 are neighbors along a dotted line
on the right-hand side. Accordingly, we have the permutations
a = (0 1)(2 5) / (0 4)(2 3), etc.
Similar relations will hold in the other pairs of diagrams
if the triangles are properly labelled.
Next: Special cases of
Up: Some planar isospectral domains
Previous: Gallery of examples
Peter Doyle
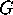 be a finite group.
Call two subgroups
be a finite group.
Call two subgroups 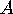 and
and 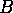 of
of 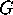 isospectral
if each element of
isospectral
if each element of 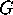 belongs to just as many conjugates of
belongs to just as many conjugates of 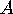 as of
as of 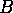 .
(This is equivalent to requiring that
.
(This is equivalent to requiring that 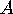 and
and 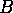 have the same number of elements in each conjugacy class of
have the same number of elements in each conjugacy class of 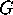 .)
Sunada's theorem states that
if
.)
Sunada's theorem states that
if 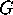 acts on a manifold
acts on a manifold 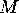 and
and 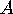 and
and 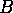 are isospectral subgroups of
are isospectral subgroups of
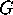 , then the quotient spaces of
, then the quotient spaces of 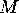 by
by 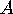 and
and 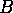 are
isospectral.
are
isospectral.
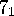 , the details are as follows.
, the details are as follows.
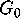 is the group of motions of the hyperbolic plane
generated by the reflections
is the group of motions of the hyperbolic plane
generated by the reflections 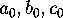 in the sides of
a triangle whose three angles are
in the sides of
a triangle whose three angles are 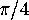 .
In Conway's orbifold notation
(see
.
In Conway's orbifold notation
(see 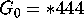 .
.
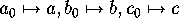 onto the finite group
onto the finite group 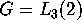 (also known as
(also known as 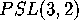 ),
the automorphism group of the projective plane of order 2.
The generators of
),
the automorphism group of the projective plane of order 2.
The generators of 
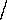 .
.
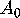 and
and 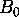 of these two groups in
of these two groups in 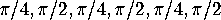 ,
and so
each of
,
and so
each of  .
.
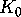 of index 168. The quotient of the hyperbolic plane by
of index 168. The quotient of the hyperbolic plane by 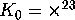 .
Deforming the metric on this 23-fold cross surface by replacing
its hyperbolic triangles by scalene Euclidean triangles yields a
cone-manifold
.
Deforming the metric on this 23-fold cross surface by replacing
its hyperbolic triangles by scalene Euclidean triangles yields a
cone-manifold 
