Next: 5.1 Triangles
Up: Part I: Two-Dimensional Geometry
Previous: 4.3 Concurrence and Collinearity
Given k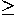 3 points
3 points 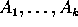 in the plane, in a certain order,
we obtain a k-sided polygon or k-gon by connecting each
point to the next, and the last to the first, with a line segment.
The points
in the plane, in a certain order,
we obtain a k-sided polygon or k-gon by connecting each
point to the next, and the last to the first, with a line segment.
The points 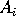 are the vertices and the segments
are the vertices and the segments 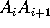 are the sides or edges of the polygon. When k=3 we have a
triangle, when k=4 we have a quadrangle or
quadrilateral, and so on (see table of regular polygons
are the sides or edges of the polygon. When k=3 we have a
triangle, when k=4 we have a quadrangle or
quadrilateral, and so on (see table of regular polygons  ).
Here we will assume that all polygons are simple: this means that
no consecutive edges are on the same line, and no two edges intersect
(except that consecutive edges intersect at the common vertex). See
Figure 1.
).
Here we will assume that all polygons are simple: this means that
no consecutive edges are on the same line, and no two edges intersect
(except that consecutive edges intersect at the common vertex). See
Figure 1.
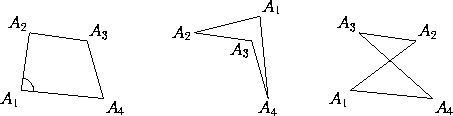
Figure 1: Two simple quadrilaterals (left and middle) and one that is
not simple (right). We will not consider non-simple polygons.
When we refer to the angle at a vertex 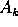 we have in mind the
interior angle (as marked in the leftmost polygon in
Figure 1). We denote this angle by the same symbol as
the vertex. The complement of
we have in mind the
interior angle (as marked in the leftmost polygon in
Figure 1). We denote this angle by the same symbol as
the vertex. The complement of 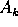 is the exterior angle at
that vertex; geometrically, it is the angle between one side and the
extension of the adjacent side. In any k-gon, the sum of the
angles equals 2(k-2) right angles, or 2(k-2)×90°:
for example, the sum of the angles of a triangle is 180°.
is the exterior angle at
that vertex; geometrically, it is the angle between one side and the
extension of the adjacent side. In any k-gon, the sum of the
angles equals 2(k-2) right angles, or 2(k-2)×90°:
for example, the sum of the angles of a triangle is 180°.
The area of a polygon whose vertices 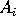 have
coordinates
have
coordinates 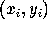 , for
, for 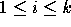 , is the absolute value of
, is the absolute value of
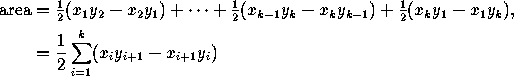
where in the sumation we take 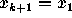 and
and 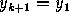 . In particular,
for a triangle we have
. In particular,
for a triangle we have
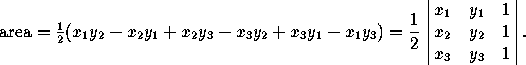
In oblique coordinates with angle 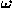 between the axes,
the area is as given above, times sin
between the axes,
the area is as given above, times sin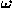 .
.
If the vertices have polar coordinates 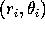 ,
for
,
for 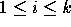 , the area is the absolute value of
, the area is the absolute value of
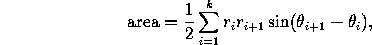
where we take 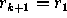 and
and 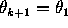 .
.
Formulas for specific polygons in terms of side lengths, angles, etc.
are given in the next sections.
Next: 5.1 Triangles
Up: Part I: Two-Dimensional Geometry
Previous: 4.3 Concurrence and Collinearity
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
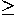 3 points
3 points 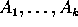 in the plane, in a certain order,
we obtain a k-sided polygon or k-gon by connecting each
point to the next, and the last to the first, with a line segment.
The points
in the plane, in a certain order,
we obtain a k-sided polygon or k-gon by connecting each
point to the next, and the last to the first, with a line segment.
The points 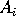 are the vertices and the segments
are the vertices and the segments 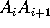 are the sides or edges of the polygon. When k=3 we have a
triangle, when k=4 we have a quadrangle or
quadrilateral, and so on (see table of regular polygons
are the sides or edges of the polygon. When k=3 we have a
triangle, when k=4 we have a quadrangle or
quadrilateral, and so on (see table of regular polygons 
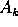 we have in mind the
interior angle (as marked in the leftmost polygon in
Figure
we have in mind the
interior angle (as marked in the leftmost polygon in
Figure 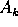 is the exterior angle at
that vertex; geometrically, it is the angle between one side and the
extension of the adjacent side. In any k-gon, the sum of the
angles equals 2(k-2) right angles, or 2(k-2)×90°:
for example, the sum of the angles of a triangle is 180°.
is the exterior angle at
that vertex; geometrically, it is the angle between one side and the
extension of the adjacent side. In any k-gon, the sum of the
angles equals 2(k-2) right angles, or 2(k-2)×90°:
for example, the sum of the angles of a triangle is 180°.
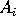 have
coordinates
have
coordinates 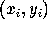 , for
, for 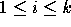 , is the absolute value of
, is the absolute value of
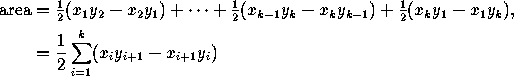
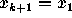 and
and 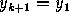 . In particular,
for a triangle we have
. In particular,
for a triangle we have
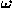 between the axes,
the area is as given above, times sin
between the axes,
the area is as given above, times sin ,
for
,
for 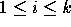 , the area is the absolute value of
, the area is the absolute value of
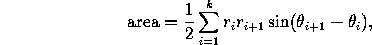
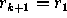 and
and 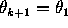 .
.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page