Halo Orbits of the Circular Restricted Three Body Problem

Surrounding each of the three collinear libration points exist families of periodic orbits. These periodic orbits, known as halo orbits, provide excellent outposts for astronomical observation. Their proximity to the Earth, and accesiblity to low-velocity space craft provide an economical opportunity to expand out knowledge about our solar system. Furthermore, the existence of stable and unstable manifolds provide cheap transport of space craft to these periodic orbits.

Unlike ordinary periodic orbits around massive singularities in the circular restricted three body problem, the families of halo orbits do not fill the six-dimensional phase space immediately surrounding the collinear libration points. If the phase space surrounding the the collinear libration points was foliated by periodic orbits, one could locate an orbit by simply starting a trajectory `close' to the libration point (in 6D phase space) and integrating until the trajectory stabilized into a periodic orbit. Given that the orbits do not completely foliate the collinear libration points, we must resort to other methods.

In order to find halo orbits in the Earth-Sun system, we first must find an analytic approximation to our family of periodic orbits. Given an approximate periodic orbit, it is necessary to try to locate an actual periodic orbit in its vicinity. In order to do this, we must look at the character of the halo orbits, and exploit the symmetries of the system.

The circular restricted three body problem, is invariant under the transformation:

that is given a trajectory:

there is guaranteed to be another trajectory:

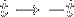
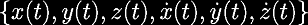
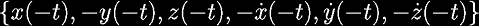
Given this symmetry, if we find a trajectory that pierces the y = 0 plane twice, such that at each piercing point, the only velocity component is in the y direction, it is guaranteed to be a periodic orbit.