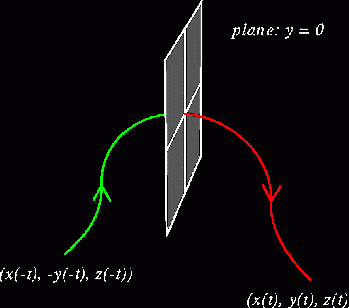
The equations of motion of the circular restricted three body problem are invariant under the substitution (x(t), y(t), z(t)) -> (x(-t), -y(-t), z(-t)). This means that given a trajectory on one side of the y = 0 plane, there exists a mirror image of that trajectory on the other side of the plane that flows backwards in time (i.e. if our original trajectory is flowing away from the plane y = 0, the mirror trajectory flows towards it). If we start a trajectory at the y = 0 plane such that it starts perpendicular to the plane, then the trajectory is "connected" to its symmetric counterpart. This fact can be exploited to find periodic orbits.

Given the red trajectory, the green one must exist due to the symmetries of the system. In this example, the two symmetric trajectories are actually two parts of the same trajectory.

In addition to the time-reversal symmetry across the y = 0 plane, there exists a mirror symmetry across the z = 0 plane (the equations of motion are invariant under the substitution: (x(t), y(t), z(t)) -> (x(t), y(t), -z(t)). This symmetry is different from the first, because the direction of flow of the mirror trajectory is the mirror of the original trajectory's flow.

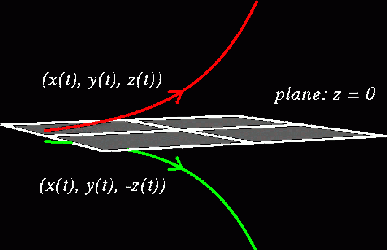
These two symmetries can be applied together to form another symmetry that has the properties of both.

Circular Restricted Three Body menu