Halo Orbits of the Circular
Restricted Three Body Problem
Halo Orbits of the Circular
Restricted Three Body Problem
 Halo Orbits of the Circular
Restricted Three Body Problem
Halo Orbits of the Circular
Restricted Three Body Problem
With this in hand, we can develop a method for finding a periodic orbit from an approximation. In 1978 Richardson developed a third order approximation to the families of halo orbits about L1, L2, L3. Since the Richardson approximations satisfy all the symmetries of the circular restricted three body problem, they all pierce the plane y = 0 perpendicularly. Using the piercing point as an initial guess to an actual periodic orbit, we have
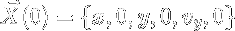
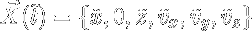 if
if
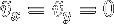
we have a periodic orbit. Thus we wish to develop a scheme such that after such an integration the x-velocity and z-velocity vanish.
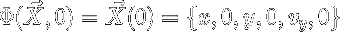
Given the trajectory associated with our initial point, phi, such that:
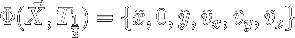
and
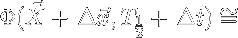
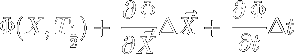
Restricting our change in the X vector to:
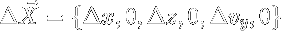
we find a new guess by solving
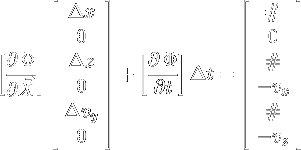
This leads to a linear system of four equations and three unknowns, allowing us to use one variable to parameterize the family of periodic orbits.
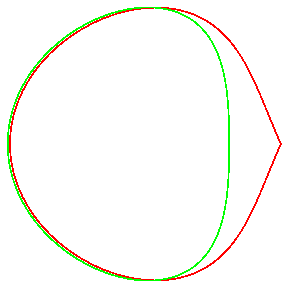
The following illustration shows a single employment of the scheme to locate periodic orbits. The red orbit is created by integrating the seed forward until it intersects the y=0 plane (line in this projection). For ease of illustration the time-reversal symmetric partner of this orbit is drawn as it's mirror image below the line y=0. This orbit is not periodic because it does not intersect the y=0 plane perpendicularly. We employ the method illustrated above to produce a new guess for the periodic orbit. The orbit corresponding to this new guess is green. One can see that this orbit intersects the y=0 plane nearly normal, indicating that this is a better approximation to the periodic orbit. This scheme is re-applied until an approximation to a periodic orbit is found to the desired accuracy.