The Fundamental Solution Matrix and Stability of Halo Orbits

The matrix d Phi/d X is important in studying the dynamics of the halo orbits. The matrix is essentially the the local linearization of the trajectory. This matrix, known as the fundamental solution matrix allows one not only to find the periodic orbits, but also examine their stability.

The fundamental solution matrix cannot be computed analytically because we do not have an analytic expression for Phi. We must resort to numeric computation of the fundamental solution matrix noting that:

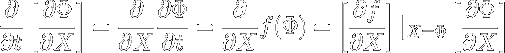
Thus we have a linear system of differential equations, which describes how the fundamental solution matrix evolves in time. Augmenting this system of equations to the six which define the field for the circular restricted three body problem we have a 42 dimensional system which allows us to compute periodic orbits. Letting M denote the fundamental solution matrix we have the following initial value problem to solve in order to get the trajectory and fundamental solution matrix associated with a particular initial condition (X_0).

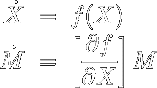
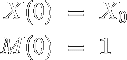
If a trajectory is periodic, than the fundamental solution matrix of a particular initial condition evaluated at a time equal to the period of the orbit (i.e. when the orbit closes on itself) is known as the monodromy matrix. The eigenvalues and eigenvectors of the monodromy matrix dictate the stability of the periodic orbit.

If we consider the period T mapping (where T is the period of a periodic orbit), we find that the image of the periodic orbit is a fixed point. Furthermore, the monodromy matrix is the local linearization of the mapping evaluated at the fixed point. This essentially means that the monodromy matrix determines the local dynamics of the system at the fixed point which represents the periodic orbit.

Because the system of differential equations is conservative, the period T mapping is flow preserving. Thus we expect the determinant of the monodromy matrix to be 1. The product of the eigenvalues must therefore be 1. It turns out to be the case that two of the eigenvalues are 1, two are complex (on the unit circle in the complex plane), and two are reciprocals. Since the local stability of the periodic orbits is determined by the evaluation of its corresponding fixed point in the mapping, the eigenvalues are associated with their eigenvectors such that if you step off the periodic orbit in a particular eigendirection, then the image of the step under the mapping is simply the original step multiplied by the corresponding eigenvalue (this analogy only applies to real eigenvalues). Thus fractional real eigenvalues represent local stable manifolds, and real eigenvalues of magnitude greater than unity represent local unstable manifolds of the fixed point under the period T mapping.

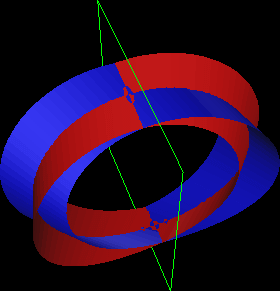
Since stability of the periodic orbit does not change along the orbit, we expect the eigenvalues of all monodromy matrices evaluated on a particular orbit to remain the same. If we evaluate the eigensystem of the monodromy matrices evaluated at every point along the orbit we find the local linearization of the stable manifold to be the the set of all eigenvectors associated with a particular stable eigenvalue (similarly true for the local unstable manifold).

The following figure shows the local unstable manifold in red , and the local stable manifold in blue for a halo orbit with a z-amplitude of approximately .0034 A.U. The green polygon represents a section of the y=0 plane which allows one to observe the time reversal symmetries across the plane (the mirror image of the unstable manifold across the y=0 plane is the stable manifold).