- From Part 1:
How do you construct a tangent line to a circle through a
point not on the circle? In this section, you observed a mathematical
fact which makes your construction work. State it explicitly.
Turn in a Sketchpad sketch of
a tangent to to a circle through an external point.
- From Part 2:
How do you construct an external tangent to two circles?
In this section, you observed a mathematical fact which makes your
construction work. State it explicitly.
Turn in a sketch tracing m as the lines containing O1 and O2 move
(see the end of Part II)
and a sketch of an external tangent to two circles.
- From Part 3: State Monge's Theorem explicitly.
Turn in your sketch of the three pairs of external tangents to three
circles, illustrating Monge's Theorem, as in the spoiler.
- From Part 4: Given two points A and A', does there exist a dilation
such that A' is the image of A under dilation? If not, what are
conditions for such a dilation to exist? If so, is such a dilation unique?
Explain.
Given four points A, A', B, and B', does there exist a dilation
such that A' is the image of A and B' is the image of B? If not, what
are conditions for such a dilation to exist? Is such a dilation unique?
Explain.
Turn in a sketch of dilating a polygon by marked ratio and a sketch
of the composition of two dilations.
- Based on your observations, you should see that the composition
of two dilations is a third dilation. Explain why the three centers of
dilation are collinear.
When are two circles related by a dilation? Is such a dilation
unique? Relate this to Part II.
Combine these results to give a logical
argument justifying Monge's Theorem.
- Read the Web page
http://www.geom.umn.edu/~banchoff/mongepappus/MP.html
and write a paragraph about a new mathematical idea you learned here.
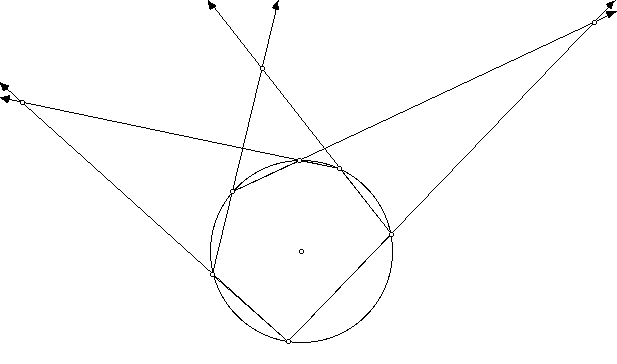
- Look at the picture below of a hexagon inscribed in a circle,
and certain lines associated to it. Does this remind you of Monge's
Theroem. Can you conjecture a theorem about such inscribed hexagons?
Support your conjecture with a sketch.
- Describe how you might explain the straight-edge and compass
construction of the tangent to a circle to your high-school students.
Write a one to two page description of such a lesson. Make a web
page for this lesson and include some Sketchpad pictures as
illustrations for the lesson.
![[HOME]](/pix/home.gif)