Next: Monge's Theorem
Up: Table of Contents
Prev: Circles and tangents

MODULE: Monge's Theorem.

Part 2: Tangents to circles.

We have found how to construct tangent lines to circles, passing through a given point either on the circle or outside of it. We now want to build on this to construct the lines tangent to two circles (of different radii) at the same time, since this is what we need for Monge's Theorem.

Draw two circles, and pick any point P on one of them. Construct the line through this point that is tangent to the other circle, using what we learned in Part I. Now drag the point P around, until the line looks tangent to both circles. Can you guess where the other external tangent will be? Can you get it by using the reflection command? Where is the mirror line?

Now, given this common tangent line, draw the radii of the two circles to the points of tangency. What angle do the radii and tangent line form? Why is that? What is true about these two radii?

The common tangent to the two circles passes then through points that have parallel radii. Let's explore this a bit more closely. Draw two circles, and any line l through the center of one of them (i.e., any line containing a radius). Now construct a parallel line through the center of the other circle. Each line intersects its circle in two opposite points. Pick the upper one (or rightmost one, or whatever) on each circle, and construct the line m through them. We know that for some particular choice of the first line l, this constructed line m would be the common tangent we are looking for. Move the line l without moving the circles, and use the "trace line" option on the Display menu to trace the locus of all the lines m you get. Do you notice anything peculiar? Can you check this? Do you see how can you construct it?

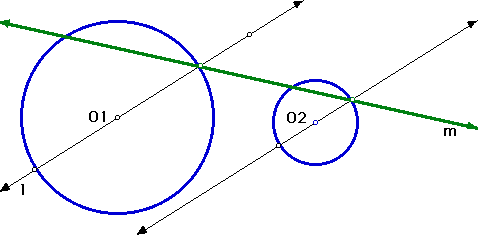
As we mentioned before, the common external tangent is one of the lines whose locus we traced above. So it too must pass through their common point, the so-called "Center of Symmetry" of the two circles. How can you use this fact to construct the common tangent lines of two circles? Can you create a script for this procedure?

Notice that when we found the center of symmetry, we picked the two upper points on each circle. What happens when we pick an upper point on one of the circles, and a lower one on the other circle? What do we get if we repeat the construction for the external tangents, but using these points now?

Next: Monge's Theorem
Up: Table of Contents
Prev: Circles and tangents
[HOME] The Geometry Center Home Page

Author: Eduardo Tabacman, revised and edited by Evelyn Sander
Comments to: webmaster@geom.umn.edu
Created: Jun 09 1996 --- Last modified: Jun 11 1996