
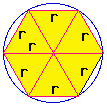
 The ancient Babylonians knew of the existence of
The ancient Babylonians knew of the existence of  - the ratio of the circumference to the diameter of any circle. The
constant they obtained, 3.125, made use of their knowledge that the
perimeter of a regular hexagon inscribed in a circle equals six times the
radius of the circle. By using this
perimeter of the inscribed hexagon as a lower bound for the
circumference of the circle, they were able to come up with their
remarkably close approximation for
- the ratio of the circumference to the diameter of any circle. The
constant they obtained, 3.125, made use of their knowledge that the
perimeter of a regular hexagon inscribed in a circle equals six times the
radius of the circle. By using this
perimeter of the inscribed hexagon as a lower bound for the
circumference of the circle, they were able to come up with their
remarkably close approximation for  circa 2000 B.C. [2, p.21].
circa 2000 B.C. [2, p.21].
During the fith century B.C., Hippias of Elis discovered the
quadratrix, a curve which could be used to determine  through a
geometric construction. Hippias'
quadratrix, could be used to "square the circle" although not in a
manner acceptable to the ancient Greek (or even modern) geometers.
"Squaring the circle" was the problem posed by the ancient Greeks in
which a square was to be constructed with area equal to that of a given
circle [2, p.40].
through a
geometric construction. Hippias'
quadratrix, could be used to "square the circle" although not in a
manner acceptable to the ancient Greek (or even modern) geometers.
"Squaring the circle" was the problem posed by the ancient Greeks in
which a square was to be constructed with area equal to that of a given
circle [2, p.40].
In the third century B.C., Archimedes of Syracuse, widely accepted as
the greatest scientific mind of antiquity, found a method whereby
 could be determined to any degree of accuracy desired. This Archimedean method for computing
could be determined to any degree of accuracy desired. This Archimedean method for computing  inscribed and circumscribed regular polygons in and
around the circle. His conception of the use of upper and lower bounds
reached the threshold of the differential calculus. The Archimedean
value of
inscribed and circumscribed regular polygons in and
around the circle. His conception of the use of upper and lower bounds
reached the threshold of the differential calculus. The Archimedean
value of  was 3 10/71 <
was 3 10/71 <  < 3 1/7 [2].
< 3 1/7 [2].
In Fifth Century A.D. China, the mathematician Tsu Chung-Chi
established that 3.1415926 <  <
3.1415927 an accuracy that
was not attained in Europe until the 16th Century [2, p.29]. The Chinese, like Archimedes
could calculate
<
3.1415927 an accuracy that
was not attained in Europe until the 16th Century [2, p.29]. The Chinese, like Archimedes
could calculate  to any degree of accuracy
desired.
to any degree of accuracy
desired.
Leonardo da Vinci (in the 16th Century) and a 17th Century Japanese document found the approximate area of a cicle by rearrangement. This method breaks the circle into equal sectors and arranges them into an approximate parallelogram. This method is not sophisticated, so it is suspected that a form of this method was used by ancient peoples to find the area of a circle [2, p.19].
The discovery of infinite series
representations for  by such mathematicians as Gregory,
Leibniz and Euler in the 17th and 18th century made it possible to
calculate ¼ to scores of digits relatively easily. By 1666 Newton
had found a way to calculate
by such mathematicians as Gregory,
Leibniz and Euler in the 17th and 18th century made it possible to
calculate ¼ to scores of digits relatively easily. By 1666 Newton
had found a way to calculate  , using his binomial theorem, to 16
decimal places using only 22 terms of an infinite series expansion [2].
, using his binomial theorem, to 16
decimal places using only 22 terms of an infinite series expansion [2].
In 1882, the German mathematician, F. Lindemann proved the number
 and its square root to be transcendental numbers, ones which
cannot be roots of polynomial equations with integer coefficients [1, p.23]. Lindemann's discovery settled the
circle squaring problem posed by the Greeks showing it to be impossible
using straight edge and compass and the rules of the ancient Greek
geometers.
and its square root to be transcendental numbers, ones which
cannot be roots of polynomial equations with integer coefficients [1, p.23]. Lindemann's discovery settled the
circle squaring problem posed by the Greeks showing it to be impossible
using straight edge and compass and the rules of the ancient Greek
geometers.
Nowdays it is easy to get more digits of  than are really useful.
What was once difficult to approximate to three or four digits is now a
trivial computer computation to hundreds of thousands of digits.
However, computing many digits of
than are really useful.
What was once difficult to approximate to three or four digits is now a
trivial computer computation to hundreds of thousands of digits.
However, computing many digits of  is a good test of a computer's
speed and accuracy. Included is the approximate
value of
is a good test of a computer's
speed and accuracy. Included is the approximate
value of  to 100,000 digits.
to 100,000 digits.
Somthing new always turns up with  . In 1995 an interesting relationship was discovered between
. In 1995 an interesting relationship was discovered between  and the
Fibonacci numbers. An exact numerical representation of
and the
Fibonacci numbers. An exact numerical representation of  can
be made using an arbitrary number of Fibonacci numbers [3]. This relationship can also be
demonstrated geometrically.
can
be made using an arbitrary number of Fibonacci numbers [3]. This relationship can also be
demonstrated geometrically.

http://www.geom.umn.edu/~huberty/math5337/groupe/overview.html Copyright © 1996-1997 Michael D. Huberty, Ko Hayashi & Chia Vang
Created: March 1996 ---- Last Modified: July 6, 1997