Rearrangement Method

Take a circle and cut it into four equal sectors. Then rearrange the sectors into a quasi-parallelogram as shown in the figure below. The area of the quasi-parallelogram can be (under)estimated by the area of the true parallelogram "inscribed" in the sectors. The "inscribed" parallelogram's area is easily found by the product of its width and height. This gives an estimate of exactly 2 for . It is apparent from the figure that this estimate will be poor, since much of the rearranged area remains outside of the "inscribed" parallelogram.

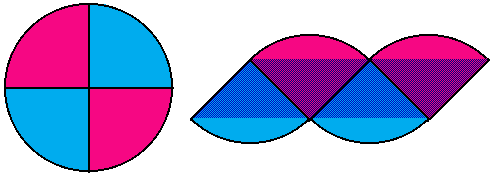
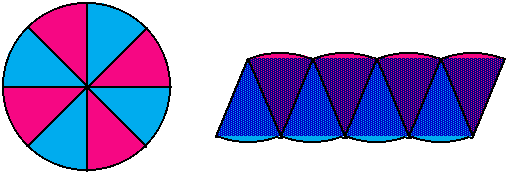
To get a better estimate, cut the circle into eight equal sectors and rearrange as shown in the figure below. It is apparent that the true parallelogram "inscribed" contains more of the circle's area than in the previous case. The estimate for is 2.829 in this case - better, but still not very accurate.

If the circle is cut into more sectors, the estimate for will improve since the rearranged sectors become more like a parallelogram. Try this using Geometer's Sketchpad rearrangment script. A Japanese document from 1689 uses this rearrangement method by slicing the circle into 32 sectors (shown below) [2, p.19]. What estimate for should the document have found?

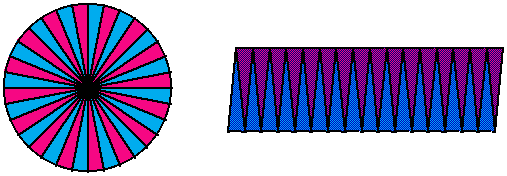
Return to Historical Overview of Pi

Go to A Slice of Pi Home Page