Archimedean Method

The Archimedean method for calculating made use of the same idea as did the Babylonian method. Archimedes, however, used the concept of making successive approximations and ascertained that the number could be determined, in principle, to a ny degree of accuracy desired. He took a circle and inscribed a regular hexagon within the circle and circumscribed one about the circle. He then, by using successive bisections, inscribed and circumscribed regular polygons within and about the circle with sides of 12, 24, 48, and finally 96 sides. The regular polygons circumscribed about the circle formed convergent upper bounds for the circumference while the regular inscribed polygons formed convergent lower bounds. The third century B.C. value which Archimedes obtained without decimal or positional notation and without trigonometry attests to his tenacity. (3 10/71 < < 3 1/7) [2].

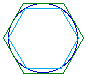
To see how an inscribed hexagon and a circumscribed hexagon gives lower and upper bounds for click on the Geometer's Sketchpad inscibed and circumscribed hexagons sketch.

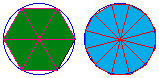
To see how approximations of improve as the inscibed polygon doubles in the number of sides click on the Geometer's Sketchpad hexagon vs dodecagon sketch.

These two ideas - inscribed and circumscribed polygons and increasing the number of sides of the polygons - are put together into the Archimedean method sketch. In this sketch you can change the angle that gives a (360°/angle)-sided polygon. (Realize that the method used allows for non-integral number of sides.) By increasing the number of sides, what happens to the lower and upper bounds for ?

Return to Historical Overview of Pi

Go to A Slice of Pi Home Page