
Recall that the Fibonacci sequence is defined by F(1) = 1, F(2) = 1, F(3) = 2, F(n) + F(n+1) = F(n+2). The following relation involving the Fibonacci numbers was proven by Ko Hayashi [3].
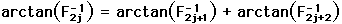
The connection to  is that arctan(1) =
is that arctan(1) =  /4. Thus
/4. Thus  can be expressed in terms of Fibonacci numbers
can be expressed in terms of Fibonacci numbers
The first three cases have been demonstrated geometrically using the Geometer's Sketchpad. (These are not really interactive sketches.)
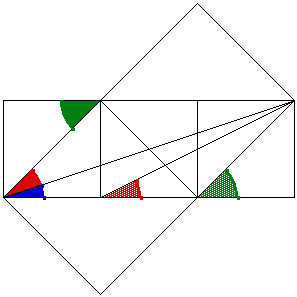
One can easily see that green angle = red angle + blue angle.
Thus we have ¼/4 = arctan(1) = arctan (1/2) + arctan(1/3).
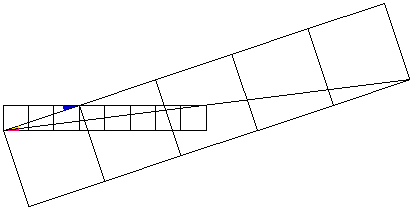
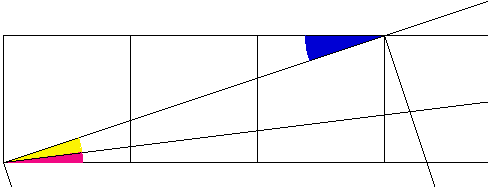
Again, it is easy see that blue angle = yellow angle + pink angle.
Thus we have arctan(1/3) = arctan (1/5) + arctan(1/8).
Combining this with the previous result yields ¼/4 = arctan(1) = arctan (1/2) + arctan (1/5) + arctan(1/8).
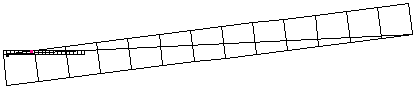

Again, it is easy see that pink angle = cyan angle + black angle.
Thus we have arctan(1/8) = arctan (1/13) + arctan(1/21).
Combining this with previous results yields ¼/4 = arctan(1) = arctan (1/2) + arctan (1/5) + arctan (1/13) + arct
an(1/21).
 as the sum of an arbitrary number of terms involving Fibonacci numbers by continuing in this manner. The repeated application of equation (*) yields
as the sum of an arbitrary number of terms involving Fibonacci numbers by continuing in this manner. The repeated application of equation (*) yields
![pi = 4*arctan(1/F(2n+2)) + 4*SUM{i=1...n}[arctan(1/F(2i+1))]](fibeq2.gif) , for any natural number n.
, for any natural number n.
Each sum starting with n =1, is an exact representation of  . One can look at four times the summation to be a partial sum with
. One can look at four times the summation to be a partial sum with
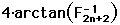
as the error term for  . The sequence of these partial sums converges to
. The sequence of these partial sums converges to  also. I.e.,
also. I.e.,
![pi = 4*SUM{i=1...infinity}[arctan(1/F(2i+1))]](fibeq3.gif) .
.Using the formula for the tangent of the sum of two angles, these relationships can be easily verified.
Return to Historical Overview of Pi

http://www.geom.umn.edu/~huberty/math5337/groupe/fibonacci.html Copyright © 1996-1997 Michael D. Huberty, Ko Hayashi & Chia Vang
Created: March 1996 ---- Last Modified: July 6, 1997