Next: Bifurcation
Up: Table of Contents
Prev: Iteration

MODULE: Dynamical Systems.

Part 4: Linear and Nonlinear Functions

Linear functions are in general easier to study than nonlinear ones. However, there is a relationship between nonlinear and linear functions. Namely, iteration of a nonlinear function near a fixed point is similar to iteration of a linear function with same slope. The following section explains this statement and shows how it can be used to predict whether a fixed point is attracting, repelling, or neutral.

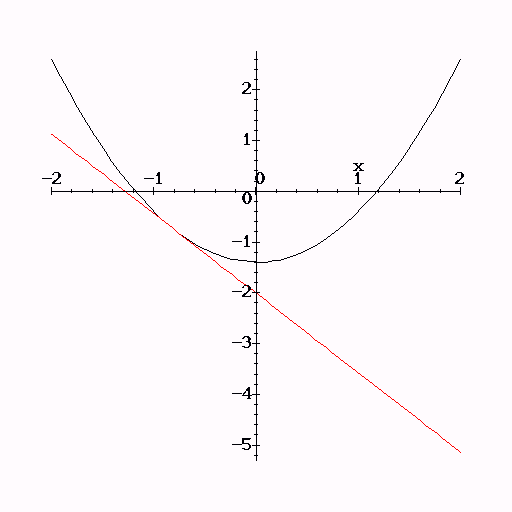
A function in the quadratic family, along with a line of the same slope through the fixed point.

Study the long term behavior of linear maps. Namely, what is the dynamics of g(x)=ax, a linear map with slope a? How does the stability of the fixed point 0 change as parameter a changes? Make sure to think about the case of a negative?

As mentioned before, near a fixed point iteration of a nonlinear map is similar to the iteration of a specific linear map. Using this, you can find a relationship between the slope of the graph at the fixed point and whether the fixed point is attracting, repelling, or neutral. First do so for the quadratic family:

For a map in the quadratic family, what is the slope of its graph at the fixed point?
Iteration of a linear map with this slope is similar to iteration of the quadratic function near the fixed point. For what values of c should fixed points for the quadratic family be attracting? Repelling? Neutral? Test your values using the Chaos Lab #2.
State the relationship between slope of the graph at the fixed point and whether the fixed point is attracting, repelling, or neutral.
Recall that in order to find period two points, you graphed the second iterate of the map. Can you find a relationship between the slope of the graph of the second iterate of the function and whether the period two points are attracting, repelling, or neutral?
Describe geometrically how your relationship might generalize to period n points.

Note: The procedure you found only works for periodic points with small periods. Although it is nice to have the condition above for whether a period n point is attracting, it becomes computationally difficult to accurately graph the nth iterate of a map as n becomes large.

Next: Bifurcation
Up: Table of Contents
Prev: Iteration

The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@www.geom.uiuc.edu
Created: Jun 09 1996 --- Last modified: Jul 31 1996