Next: Linear and Nonlinear Functions
Up: Table of Contents
Prev: Parametrized Families and Periodic Points

MODULE: Dynamical Systems.

Part 3: Iteration

The iteration feature of the Chaos Lab shows iterates visually using something called graphical iteration. It starts by showing a graph of the function y=f(x) and a graph of the identity function y=i(x). When you choose a value z to iterate, the program draws a vertical line to the first iterate, (z,f(z)). Then it draws a horizontal line to the point (f(z),f(z)) on the graph of the identity function. This allows iteration to be repeated, because drawing a vertical line from (f(z),f(z)) to the graph of f gives the point (f(z), f(f(z))), the second iterate. Repeating this process gives all the iterates of z. For the quadratic family, pick a c value between 0 and -2, and iterate as follows:

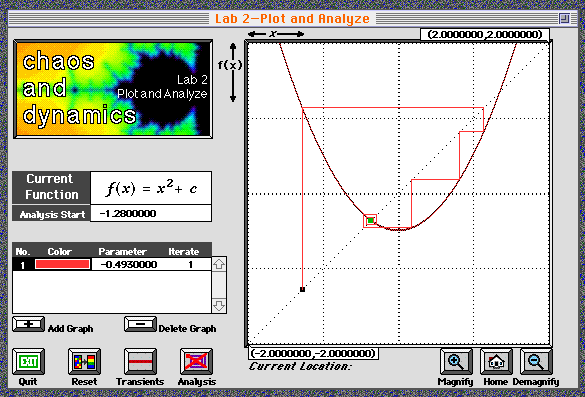
This picture shows graphical iteration for a member of the quadratic family.

Instructions to Iterate

Double click on the x value for which you want to start the iteration. Your choice will appear in the Analysis Start box.
Alternatively, edit the Analysis Start box to your desired initial x value.

Methods to Study Iterates

Since we are interested in long term behavior, we only care about how the iterates behave after a long time. The initial iterates are irrelevant for long term behavior, and are called transients. Click on the Transients button to remove these transients. Clicking on it again toggles back to seeing all iterates.
To get a closer look at a region, use the mouse to select a region, and click on the Magnify button.

From Part 1, which of the fixed points are attracting for c=0? Repelling? Here is a picture representing the eventual behavior of all points on the line for c=0. The arrows represent the direction that points go after iteration.

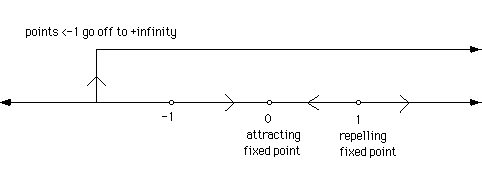
Draw a qualitative diagram for the eventual behavior of all points for c=-0.4. Your diagram should resemble the picture above, but it does not need to have exact values of fixed and periodic points. The idea is to compare pictures qualitatively. Use the techniques from the Methods to Study Iterates section above to formulate the diagram.
Draw a similar diagram for c=-1.1. As you investigate, magnify the region near the smaller fixed point. What has happened? What is the period of the attracting set? In some way, indicate the period of all the periodic points. Also remember to indicate what happens to large negative values of x.
Draw a similar diagram for c=-1.3. What is the period of the attracting orbit here? Indicate in which order the points in the orbit occur.
What happens for c=-2?

Now that you have investigated dynamics for some select values of c, think about the following ideas for the entire family f_c.

The dynamics of a function is a qualitative description of the eventual behavior of all points on the line. This includes information such as the number and relative placement of fixed and periodic points and whether they are attracting, repelling, or neutral. You should have found that at each of the values c= -0.4, -1.1, -1.3, and -2, the dynamics is qualitatively distinct.

Definition (Bifurcation): A change in the dynamics for a certain c is called a bifurcation.

Does every value c give different dynamics? Look at some intermediate values between c=-0.4 and c=-1.1. Is the dynamics at each intermediate value qualitatively distinct from the dynamics you have already studied? If not, what happens?
Between c=-0.4 and c=-1.1, at approximately what c value does a bifurcation occur?

In the next section, we address the question: Is there any way to find this bifurcation it exactly?

Next: Linear and Nonlinear Functions
Up: Table of Contents
Prev: Parametrized Families and Periodic Points

The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@www.geom.uiuc.edu
Created: Jun 09 1996 --- Last modified: Jul 31 1996