Next: Questions on Dynamical Systems
Up: Table of Contents
Prev: Linear and Nonlinear Functions

MODULE: Dynamical Systems.

Part 5: Bifurcation

Now that you have had a chance to think about bifurcations, you will look at a new graph called the orbit diagram. This is a way of testing the eventual behavior of bounded orbits (that is, the orbits which do not just go off to infinity.) Consider the following conclusions from the previous section: for f(x)=x^2, orbits of points between -1 and 1 converge to the fixed point 0. For some negative value of c, both fixed points are repelling, and an attracting period two point has appeared. This section describes another method of finding bifurcations using Chaos Lab #3.

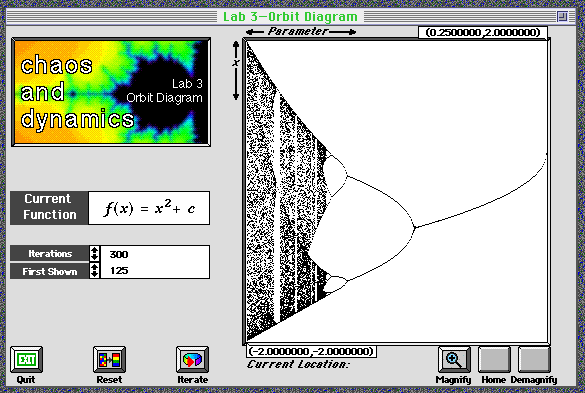
The orbit diagram for the quadratic family seen in Chaos Lab #3.

The picture above is called the orbit diagram for the quadratic family f_c(x)=x^2+c. Here is how it has been plotted: Each horizontal value corresponds to a value of the parameter c. The vertical values correspond to the values of iterates. The program begins by iterating but does not display for the number of iterates in the First Shown box. As before, this removes transients. It then displays the number of iterates in the Iterations box.

Notice that for c near 0, there is only a single point for each value of c. This corresponds to the fact that for these values of c, the fixed point is attracting. Use the following procedure to study the orbit diagram and answer the questions below.

How to Study the Orbit Diagram

Start Chaos Lab #3. Change the current function to quadratic, and click on the Iterate button.
To get a picture more accurately reflecting the eventual attracting behavior, increase the numbers in the First Shown and Iterations boxes.
To look at a particular area, select the area with your mouse, and click on the Magnify button.

Questions

Between -0.4 and -1.1, the orbit diagram curve splits into two branches. How does this relate to what you saw in Chaos Lab #2? Why are there two branches now? What do they correspond to? (Hint: What was the eventual behavior of points in this region?)
Investigate further bifurcations as c decreases. Describe the sequence of bifurcations. In other words, how does the period of the attracting set change at each bifurcation?
How would you describe the orbit diagram near c=-2?

Next: Questions on Dynamical Systems
Up: Table of Contents
Prev: Linear and Nonlinear Functions

The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@www.geom.uiuc.edu
Created: Jun 09 1996 --- Last modified: Jul 31 1996