![[More]](pix/Link.gif) .
.
![[More]](pix/Link.gif)
The boundary curves mentioned in (3) are called
top cycles, and they
play a key role in understanding tight immersions. Note that a
top cycle is an embedded, planar, convex curve, and that every top
cycle has an
orientable neighborhood
![[More]](pix/Link.gif) .
.
If a tight immersion of a connected surface has no top cycles, then it is necessarily a sphere, since in this case the image of the M+ region is all of the convex envelope (and there is no M- region). So a tight immersion of the projective plane must have at least one top cycle.
There is only one class of embedded curves on the projective plane that do not bound regions; but curves in this class have non-orientable neighborhoods (the neighborhood is a Möbius band, as in the diagram below), and so they can not be top cycles.
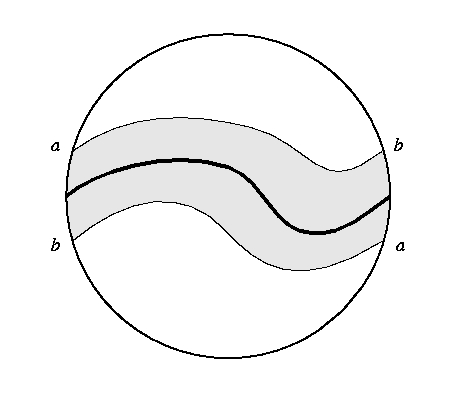
This is a contradiction, so there can be no tight immersion of the real projective plane.
![[Right]](pix/Right.gif) There is no tight Klein bottle
There is no tight Klein bottle
![[Left]](pix/Left.gif) Non-orientable tight surfaces
Non-orientable tight surfaces
![[Up]](pix/Up.gif) Kuiper's initial question
Kuiper's initial question
7/21/94 dpvc@geom.umn.edu --
The Geometry Center