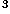 +bx
+bx +cx+d, with a
+cx+d, with a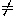 0. This curve is a
(general) cubic parabola (Figure 1). It is
symmetric with respect to the point B where x=-b/3a.
0. This curve is a
(general) cubic parabola (Figure 1). It is
symmetric with respect to the point B where x=-b/3a.
Next: 8.2 Roulettes (Spirograph Curves)
Up: 8 Special Plane Curves
Previous: 8 Special Plane Curves
Curves that can be given in implicit form as f(x,y)=0, where f is a polynomial, are called algebraic. The degree of f is called the degree or order of the curve. Thus conics (Section 7) are algebraic curves of degree two. Curves of degree three already have a great variety of shapes, and only a few common ones will be given here.
The simplest case is when the curve is the graph of a polynomial of
degree three: y=ax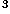 +bx
+bx +cx+d, with a
+cx+d, with a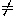 0. This curve is a
(general) cubic parabola (Figure 1). It is
symmetric with respect to the point B where x=-b/3a.
0. This curve is a
(general) cubic parabola (Figure 1). It is
symmetric with respect to the point B where x=-b/3a.
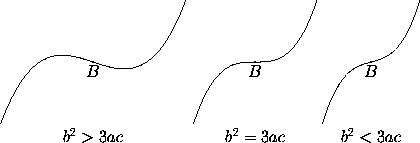
Figure 1: The general cubic parabola for a>0. For a<0, reflect in
a horizontal line.
The semicubic parabola (Figure 2, left) has
equation y =kx
=kx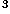 ; by proportional scaling one can take k=1.
; by proportional scaling one can take k=1.
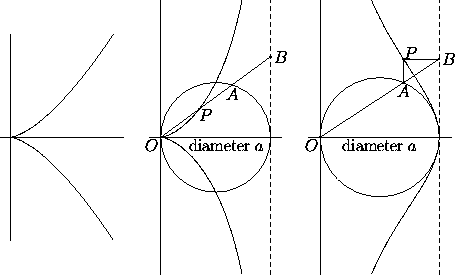
Figure 2: The semicubic parabola, the cissoid of Diocles, and the witch
of Agnesi
This curve should not be confused with the cissoid of Diocles
(Figure 2, middle), which has equation
(a-x)y =x
=x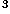
with a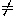 0. The latter is asymptotic to the line x=a, while the
semicubic parabola has no asymptotes. The cissoid's points are
characterized by the equality OP=AB in Figure 2,
right. One can take a=1 by proportional scaling.
0. The latter is asymptotic to the line x=a, while the
semicubic parabola has no asymptotes. The cissoid's points are
characterized by the equality OP=AB in Figure 2,
right. One can take a=1 by proportional scaling.
More generally, any curve of degree three with equation
(x-x )y
)y =f(x), where f is a polynomial, is symmetric with
respect to the x-axis and asymptotic to the line x=x
=f(x), where f is a polynomial, is symmetric with
respect to the x-axis and asymptotic to the line x=x . In
addition to the cissoid, the following particular cases are important:
. In
addition to the cissoid, the following particular cases are important:
 =a
=a (a-x), with a
(a-x), with a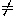 0, and is
characterized by the geometric property shown in
Figure 2, right. The same property provides the
parametric representation x=a(1+sin 2
0, and is
characterized by the geometric property shown in
Figure 2, right. The same property provides the
parametric representation x=a(1+sin 2 ), y=a tan
), y=a tan  .
Once more, proportional scaling reduces to the case a=1.
.
Once more, proportional scaling reduces to the case a=1.
 =-x
=-x (
(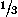 x+a), with a
x+a), with a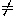 0 (reducible to a=1
by proportional scaling). By rotating 135°(right) we get the
alternative and more familiar equation x
0 (reducible to a=1
by proportional scaling). By rotating 135°(right) we get the
alternative and more familiar equation x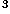 +y
+y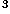 =cxy, where
c=
=cxy, where
c=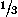
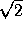 a. The folium of Descartes is a rational
curve, this is, it has a parametric representation by rational
functions. In the tilted position such a representation is
x=ct/(1+t
a. The folium of Descartes is a rational
curve, this is, it has a parametric representation by rational
functions. In the tilted position such a representation is
x=ct/(1+t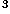 ), y=ct
), y=ct /(1+t
/(1+t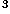 ) (so that t=y/x).
) (so that t=y/x).
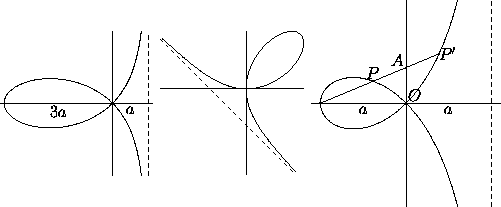
Figure 3: The folium of Descartes in two positions, and the strophoid.
 =-x
=-x (x+a), with a
(x+a), with a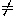 0
(reducible to a=1 by proportional scaling). It satisfies the
property AP=AP'=OA in Figure 3, right; this means
that POP' is a right angle. The strophoid has the polar
representation r=-a cos 2
0
(reducible to a=1 by proportional scaling). It satisfies the
property AP=AP'=OA in Figure 3, right; this means
that POP' is a right angle. The strophoid has the polar
representation r=-a cos 2 sec
sec  , and the rational
parametric representation x=a(t
, and the rational
parametric representation x=a(t -1)/(t
-1)/(t +1), y=at(t
+1), y=at(t -1)/(t
-1)/(t +1)
(so that t=y/x).
+1)
(so that t=y/x).
Among the important curves of degree four are the following:
 . If the foci are on the x-axis and equidistant
from the origin, the curve's equation is
(x
. If the foci are on the x-axis and equidistant
from the origin, the curve's equation is
(x +y
+y +a
+a )
) -4a
-4a x
x =k
=k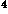 . Changes in a correspond to
rescaling, while the value of k/a controls the shape: the curve has
one smooth piece, one piece with a self-intersection, or two pieces
depending on whether k is greater than, equal to, or smaller than
a (Figure 4). The case k=a is also known as the
lemniscate (of Jakob Bernoulli); the equation reduces to
(x
. Changes in a correspond to
rescaling, while the value of k/a controls the shape: the curve has
one smooth piece, one piece with a self-intersection, or two pieces
depending on whether k is greater than, equal to, or smaller than
a (Figure 4). The case k=a is also known as the
lemniscate (of Jakob Bernoulli); the equation reduces to
(x +y
+y )
) =a
=a (x
(x -y
-y ), and upon a 45° rotation to
(x
), and upon a 45° rotation to
(x +y
+y )
) =2a
=2a xy. Each Cassini's oval is the section of a torus of
revolution by a plane parallel to the axis of revolution.
xy. Each Cassini's oval is the section of a torus of
revolution by a plane parallel to the axis of revolution.
Figure 4: Cassini's ovals for k=.5a, .9a, 1.1a
and 1.5a
(from the inside to the outside). The foci (dots) are at x=a and
x=-a. The black curve, k=a, is also called Bernoulli's
lemniscate.
r=a sec  +k.
+k.
Once more, a is a scaling parameter, and the value of
k/a controls the shape: when k>-a the curve is smooth,
when
k=-a
there is a cusp, and when k<-a there is a self-intersection. The
curves for k and -k can also be considered two leaves of the same
conchoid, with cartesian equation (x-a) (x
(x +y
+y )=k
)=k x
x .
.
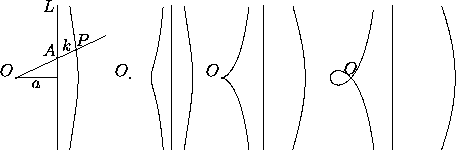
Figure 5: Defining property of the conchoid of Nichomedes (left), and
curves for k=±.5a,
k=±a, and k=±1.5a (right).
r=a cos  + k,
+ k,
and cartesian equation (x +y
+y -ax)
-ax) =k
=k (x
(x +y
+y ). The
value of k/a controls the shape, and there are two particularly
interesting cases. For k=a we get a cardioid (see also
Figure 8.2.2
, right).
For a=½k we get a curve that can be
used to trisect an arbitrary angle
). The
value of k/a controls the shape, and there are two particularly
interesting cases. For k=a we get a cardioid (see also
Figure 8.2.2
, right).
For a=½k we get a curve that can be
used to trisect an arbitrary angle 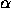 : if we draw a line
L through the center of the circle C and making an angle
: if we draw a line
L through the center of the circle C and making an angle 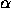
with the positive x-axis, and if we call P the intersection of L
with the limaçon a=2k, the line from O to P makes an angle
 with L.
with L.
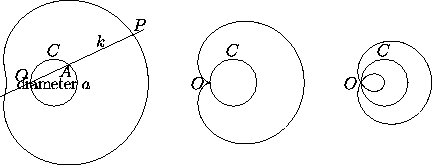
Figure 6: Defining property of the limaçon of Pascal (left), and
curves for k=1.5a, k=a, and k=.5a (right).
The middle curve is the cardioid, the one on the right a trisectrix.
Hypocycloids and epicycloids with rational ratio (see next section) are also algebraic curves, generally of higher degree.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.