 /(4a) on the x-axis with pole
the focus of the parabola (that is, P=(0,a) in the initial
position). The
catenary is the shape taken under the action of gravity by a chain or
string of uniform density whose ends are held in the air.
/(4a) on the x-axis with pole
the focus of the parabola (that is, P=(0,a) in the initial
position). The
catenary is the shape taken under the action of gravity by a chain or
string of uniform density whose ends are held in the air.
Next: 8.3 Spirals
Up: 8 Special Plane Curves
Previous: 8.1 Algebraic Curves
Suppose given a fixed curve C and a moving curve M, which rolls on C without slipping. The curve drawn by a point P kept fixed with respect to M is called a roulette, of which P is the pole.
The most important examples of roulettes arise when M is a circle
and C is a straight line or a circle, but an interesting additional
example is provided by the catenary y=a cosh(x/a), which
arises by rolling the parabola y=x /(4a) on the x-axis with pole
the focus of the parabola (that is, P=(0,a) in the initial
position). The
catenary is the shape taken under the action of gravity by a chain or
string of uniform density whose ends are held in the air.
/(4a) on the x-axis with pole
the focus of the parabola (that is, P=(0,a) in the initial
position). The
catenary is the shape taken under the action of gravity by a chain or
string of uniform density whose ends are held in the air.
A circle rolling on a straight line gives a trochoid, with the cycloid as a special case when the pole P lies on the circle (Figure 1). If the moving circle M has radius a and the distance from the pole P to the center of M is k, the trochoid has the parametric equation
x=a -k sin
-k sin  ,
y=a-k cos
,
y=a-k cos  .
.
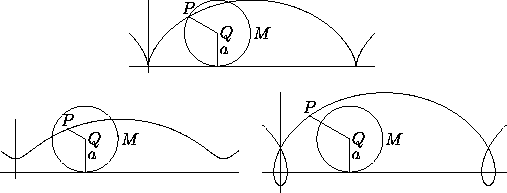
Figure 1: Cycloid (top) and trochoids with k=.5a and
k=1.5a, where k is the distance PQ from the center
of the rolling circle to the pole.
The cycloid, therefore, has parametric equation
x=a( - sin
- sin  ),
),
y=a(1- cos  ).
).
One can eliminate  to get x as a
(multivalued) function of y, which takes the following form for the
cycloid:
to get x as a
(multivalued) function of y, which takes the following form for the
cycloid:
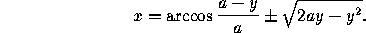
The length of one arch of the cycloid is 8a, and the area under the
arch is 3 a
a .
.
A trochoid is also called a curtate cycloid when k<a (that is, when P is inside the circle) and a prolate cycloid when k>a.
A circle rolling on another circle and exterior to it gives an epitrochoid. If a is the radius of the fixed circle, b that of the rolling circle and k is the distance from P to the center of the rolling circle, the parametric equation of the epitrochoid is
x=(a+b) cos  - k cos ((1+a/b)
- k cos ((1+a/b) ),
),
y=(a+b) sin  - k sin ((1+a/b)
- k sin ((1+a/b) ).
).
These equations assume that at the start everything is aligned along the positive x-axis, as in Figure 2, left.
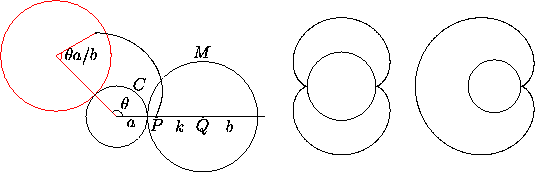
Figure 2: Left: Initial configuration for epicycloid (black) and
configuration at parameter value  (red). Middle: epicycloid
with b=½a (nephroid). Right: epicycloid with b=a (cardioid).
(red). Middle: epicycloid
with b=½a (nephroid). Right: epicycloid with b=a (cardioid).
Usually one considers the case when a/b is a rational number, say a/b=p/q where p and q are relatively prime. Then the rolling circle returns to its original position after rotating q times around the fixed circle, and the epitrochoid is a closed curve---in fact, an algebraic curve. One also usually takes k=b, so that P lies on the rolling circle; the curve in this case is called an epicycloid. The middle diagram in Figure 2 shows the case b=k=½a, called the nephroid; this curve is the cross section of the caustic of a spherical mirror. The diagram on the right shows the case b=k=a, which gives the cardioid (compare Figure 8.1.6 , middle).
Hypotrochoids and hypocycloids are defined in the same way as epitrochoids and epicycloids, but the rolling circle is inside the fixed one. The parametric equation of the hypotrochoid is
x=(a-b) cos  + k cos ((a/b-1)
+ k cos ((a/b-1)  ),
),
y=(a-b) sin  - k sin ((a/b-1)
- k sin ((a/b-1)  ),
),
where the letters have the same meaning as for the epitrochoid. Usually one takes a/b rational and k=b. There are several interesting particular cases:
 a gives the deltoid (Figure 3, left), which
has the algebraic equation
a gives the deltoid (Figure 3, left), which
has the algebraic equation
(x +y
+y )
) -8ax
-8ax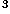 +24axy
+24axy +18a
+18a (x
(x +y
+y )-27a
)-27a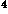 =0.
=0.
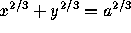 .
The figure illustrates another property of the astroid: its tangent
intersects the coordinate axes at points that are always the same
distance a apart. Otherwise said, the astroid is the envelope of a
moving segment of fixed length whose endpoints are constrained to lie
on the two coordinate axes.
.
The figure illustrates another property of the astroid: its tangent
intersects the coordinate axes at points that are always the same
distance a apart. Otherwise said, the astroid is the envelope of a
moving segment of fixed length whose endpoints are constrained to lie
on the two coordinate axes.
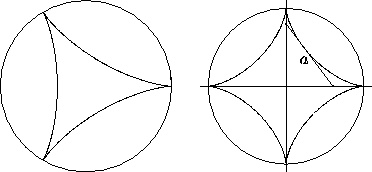
Figure 3: The hypocycloids with a=3b (deltoid) and
a=4b (astroid).
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.