Names for features of symmetrical patterns
Next: Names for symmetry
Up: Geometry and the Imagination
Previous: Symmetry and orbifolds
We begin by introducing names for certain features that may occur in symmetrical
patterns. To each such feature of the pattern,
there is a corresponding feature of the quotient orbifold,
which we will discuss later.
A mirror is a line about which the pattern has mirror symmetry.
Mirrors are perhaps the easiest features to pick out by eye.
At a crossing point, where two or more mirrors cross,
the pattern will necessarily also have rotational symmetry.
An  -way crossing point is one where precisely
-way crossing point is one where precisely  mirrors meet.
At an
mirrors meet.
At an  -way crossing point, adjacent mirrors meet at an angle of
-way crossing point, adjacent mirrors meet at an angle of 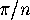 .
(Beware: at a 2-way crossing point,
where two mirrors meet at right angles,
there will be 4 slices of pie coming together.)
.
(Beware: at a 2-way crossing point,
where two mirrors meet at right angles,
there will be 4 slices of pie coming together.)
We obtain a mirror string by starting somewhere on a mirror
and walking along the mirror to the next crossing point,
turning as far right as we can so as to walk along another mirror,
walking to the next crossing point on it, and so on.
(See figure 19.)
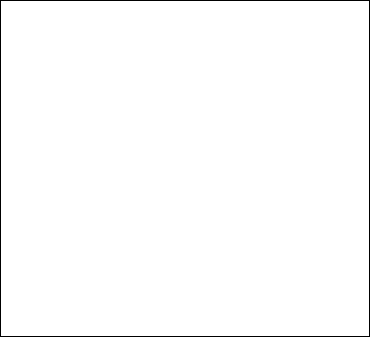
Figure 19: The quotient billiard orbifold.
Suppose that you walk along a mirror string
until you first reach a point exactly like the one you started from.
If the crossings you turned at were (say)
a 6-way, then a 3-way, and then a 2-way crossing,
then the mirror string would be of type 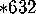 , etc.
As a special case,
the notation
, etc.
As a special case,
the notation  denotes a mirror that meets no others.
denotes a mirror that meets no others.
For example, look at a standard brick wall.
There are horizontal mirrors that each bisect a whole row of bricks,
and vertical mirrors that pass through bricks and cement
alternately.
The crossing points, all 2-way, are of two kinds:
one at the center of a brick,
one between bricks.
The mirror strings have four corners,
and you might expect that their type would be 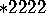 .
However, the correct type is
.
However, the correct type is 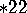 .
The reason is that after going only half way round, we come to a point
exactly like our starting point.
.
The reason is that after going only half way round, we come to a point
exactly like our starting point.
In the quotient orbifold, a mirror string of type 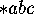 becomes a boundary wall,
along which there are corners of angles
becomes a boundary wall,
along which there are corners of angles 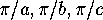 .
We call this a mirror boundary of type
.
We call this a mirror boundary of type 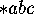 .
For example, a mirror boundary with no corners at all has type
.
For example, a mirror boundary with no corners at all has type  .
The quotient orbifold of a brick wall has a mirror boundary with just
two right-angled corners, type
.
The quotient orbifold of a brick wall has a mirror boundary with just
two right-angled corners, type 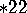 .
.
Any point around which a pattern has rotational symmetry is called
a rotation point.
Crossing points are rotation points, but there may also be others.
A rotation point that does NOT
lie on a mirror is called a
gyration point.
A gyration point has order  if the smallest angle of any rotation
about it is
if the smallest angle of any rotation
about it is 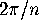 .
.
For example, on our brick wall there is an order 2 gyration point
in the middle of the rectangle outlined by any mirror string.
In the quotient orbifold, a gyration point of order  becomes a cone point
with cone angle
becomes a cone point
with cone angle 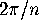 .
.
Next: Names for symmetry
Up: Geometry and the Imagination
Previous: Symmetry and orbifolds
Peter Doyle
 -way crossing point is one where precisely
-way crossing point is one where precisely  mirrors meet.
At an
mirrors meet.
At an  -way crossing point, adjacent mirrors meet at an angle of
-way crossing point, adjacent mirrors meet at an angle of 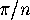 .
(Beware: at a 2-way crossing point,
where two mirrors meet at right angles,
there will be 4 slices of pie coming together.)
.
(Beware: at a 2-way crossing point,
where two mirrors meet at right angles,
there will be 4 slices of pie coming together.)
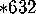 , etc.
As a special case,
the notation
, etc.
As a special case,
the notation  denotes a mirror that meets no others.
denotes a mirror that meets no others.
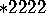 .
However, the correct type is
.
However, the correct type is 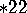 .
The reason is that after going only half way round, we come to a point
exactly like our starting point.
.
The reason is that after going only half way round, we come to a point
exactly like our starting point.
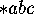 becomes a boundary wall,
along which there are corners of angles
becomes a boundary wall,
along which there are corners of angles 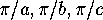 .
We call this a mirror boundary of type
.
We call this a mirror boundary of type 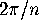 .
.