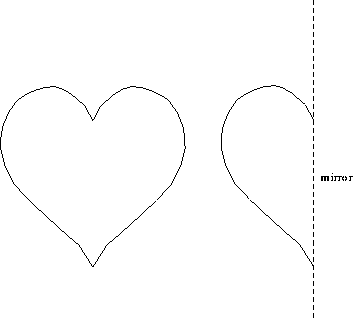
Figure 10: A heart is obtained by folding a sheet of paper in half, and cutting out half a heart. The half-heart is the orbifold for the pattern. A heart can also be recreated from a half-heart by holding it up to a mirror.
Given a symmetric pattern, what happens when you identify equivalent points? It gives an object with interesting topological and geometrical properties, called an orbifold.
The first instance of this is an object with bilateral symmetry, such as a (stylized) heart. Children learn to cut out a heart by folding a sheet of paper in half, and cutting out half of the pattern. When you identify equivalent points, you get half a heart.
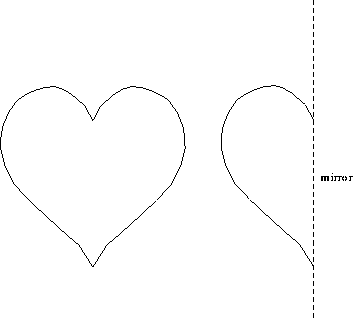
Figure 10: A heart is obtained by
folding a sheet of paper in half, and cutting out half a heart. The
half-heart is the orbifold for the pattern. A heart can also be recreated
from a half-heart by holding it up to a mirror.
A second instance is the paper doll pattern. Here, there are two different fold lines. You make paper dolls by folding a strip of paper zig-zag, and then cutting out half a person. The half-person is enough to reconstruct the whole pattern. The quotient orbifold is a half-person, with two mirror lines.
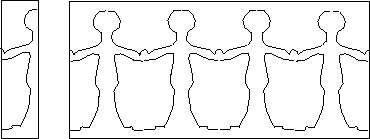
Figure 11: A string of paper dolls
A wave pattern is the next example. This pattern repeats horizontally, with no reflections or rotations. The wave pattern can be rolled up into a cylinder. It can be constructed by rolling up a strip of paper around a cylinder, and cutting a single wave, through several layers, with a sharp knife. When it is unrolled, the bottom part will be like the waves.
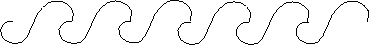
Figure 12: This wave pattern repeats horizontally, with no reflections
or rotations. The quotient orbifold is a cylinder.
When a pattern repeats both horizontally and vertically, but without reflections or rotations, the quotient orbifold is a torus. You can think of it by first rolling up the pattern in one direction, matching up equivalent points, to get a long cylinder. The cylinder has a pattern which still repeats vertically. Now coil the cylinder in the other direction to match up equivalent points on the cylinder. This gives a torus.
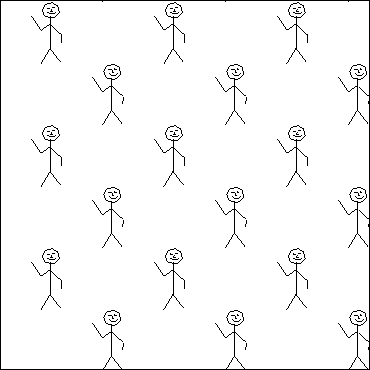
Figure 13: This pattern has quotient orbifold a torus.
It repeats both horizontally and vertically, but without any reflections
or rotations. It can be rolled up horizontally to form a cylinder,
and then vertically (with a twist) to form a torus.
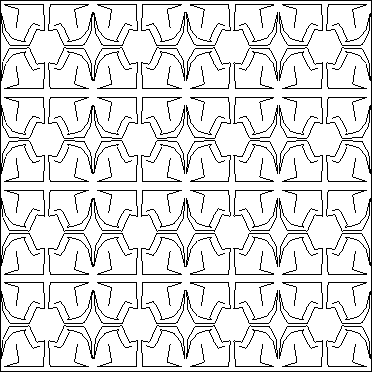
Figure 14: The quotient orbifold is a rectangle,
with four mirrors around it.

Figure 15: The quotient orbifold is an annulus,
with two mirrors, one on each boundary.

Figure 16: The quotient orbifold is a Moebius band,
with a single mirror on its single boundary.

Figure 17: The quotient orbifold is a 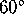 ,
,
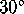 ,
, 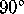 triangle, with three mirrors from sides.
triangle, with three mirrors from sides.

Figure 18: This pattern has rotational symmetry about
various points, but no reflections. The rotations are of order 6,
3 and 2. The quotient orbifold is a triangular pillow, with
three cone points.
Using the notation we have discussed, try to figure out the description of the various pieces of fabric we have handed out. That is, locate the mirror strings, gyration points, cone points, etc. Find the orders of the gyration points and the cone points.