The Euler Number
Next: Symmetry and orbifolds
Up: Geometry and the Imagination
Previous: Summary
If we have a polyhedron, we can compute its Euler number,
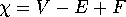 . In fact, we computed Euler numbers
ad delectam.
Why did we do this? One reason
is that they are is easy to compute. But that is not obviously a compelling
reason for doing anything in mathematics. The real reason is that it
is an invariant of the surface (it does not depend upon what map one puts
on the surface) and because it is connected to a whole array of other
properties a surface might have that one might notice while trying to describe
it.
. In fact, we computed Euler numbers
ad delectam.
Why did we do this? One reason
is that they are is easy to compute. But that is not obviously a compelling
reason for doing anything in mathematics. The real reason is that it
is an invariant of the surface (it does not depend upon what map one puts
on the surface) and because it is connected to a whole array of other
properties a surface might have that one might notice while trying to describe
it.
One easy example of this is Descartes' formula. If one looks at
a polyhedral surface and makes a naive attempt to
describe it visually, one might try to describe how pointy
the surface is. A more sophisticated way to describe how pointy
a surface is at a vertex is to compute the angular defect at the vertex, that is
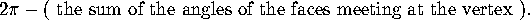
When we investigated how pointy a polyhedron was, summing over all
of the vertices to obtain the total angular defect

, we discovered that there was a direct connection
between pointyness and Euler Number:
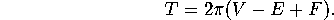
Although projecting Conway's image onto the celestial sphere was fun, again it
was not in and of itself a mathematically valuable exercise. The point
was to get a feel for the Gauss map. The Gauss map is used to project
a surface onto the celestial sphere. For a polyhedron, we saw that, if one traced a path that
remained on a flat face, the Gauss image of that path was really a point.
We saw that if we traced a path that went around a vertex, the Gauss image
was a spherical polygon. If three edges met at the given
vertex, the Gauss image traced out a spherical triangle whose interior
could be thought of as the image of that vertex. Moreover, the angles of the triangle were
the supplements of the vertex angles. Using the formula for
the area of a spherical triangle, namely
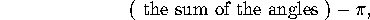
if the vertex angles were

, the area
of the Gauss image of a path around the vertex would be
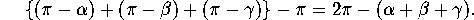
The right hand side of this formula is just the angular defect at the vertex.
Thus if we add up the areas of the images of path about all of the
vertices, we obtain the total defect

of the original surface.
Since no other parts of the image contribute to the area, we have shown that
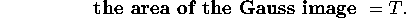
Exploiting the earlier connection, we can also say
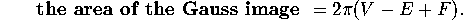
This is known as the Gauss-Bonnet formula.
Again, cutting up kale and cabbage was fun and the tape of Thurston and
Conway sticking potato peel to the chalkboard will become a classic, but
there was a serious mathematical purpose behind it. If one looks at a surface
and wants to try to describe it visually, one might want to describe it by
telling how curly it is. While the surface of a
cylinder, for example, does not look visually as though it
curves and bends very much, the surface of a trumpet does.
Peeling a surface, that is, removing a thin
strip from around a portion of the surface and then
seeing how much the angle between the ends of the strip opens up
(or closes around)
as it is
laid flat quantifies the curviness of
the portion of the surface surrounded by the strip. Mathematically,
this is called the integrated curvature of that portion of the surface.
When we sum over portions that amount to the whole surface,
we get the total Gaussian curvature of the surface.
Lets apply these ideas to a polyhedron. In particular, we might
consider a strip of polyhedron peel that just goes around one vertex
of a polyhedron.
Then we would find that the path opens up by an angle equal to the defect at that vertex, and so for such a path
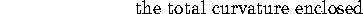
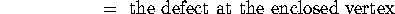
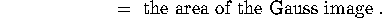
For a path that goes around several vertices the curvature is the sum of the
defects of all the surrounded vertices. Thus for a polyhedron,
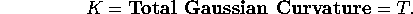
To pass from a polyhedral surface to a smooth surface and to define curvature
with mathematical precision, one needs to use integration in the definition
for  . But the conceptual idea is still the same. Any curved surface can be approximated by a polyhedral one with lots and
lots of vertices. The curvature of the surface within a path (a smooth
piece of peel) is then very nearly equal to the sum of the defects
at all the encircled vertices. By a technical limiting argument that
involves integrals to give a precise meaning to curvature,
. But the conceptual idea is still the same. Any curved surface can be approximated by a polyhedral one with lots and
lots of vertices. The curvature of the surface within a path (a smooth
piece of peel) is then very nearly equal to the sum of the defects
at all the encircled vertices. By a technical limiting argument that
involves integrals to give a precise meaning to curvature, 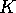 ,
we find that for any surface
,
we find that for any surface
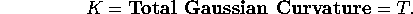
- There are many other connections between these four
concepts. Can you suggest any more?
(This is also a discussion question for the gang of four.)
-
The number of handles on a surface is another visual characteristic.
How does this relate to the total curvature?
Next: Symmetry and orbifolds
Up: Geometry and the Imagination
Previous: Summary
Peter Doyle
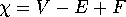 . In fact, we computed Euler numbers
ad delectam.
Why did we do this? One reason
is that they are is easy to compute. But that is not obviously a compelling
reason for doing anything in mathematics. The real reason is that it
is an invariant of the surface (it does not depend upon what map one puts
on the surface) and because it is connected to a whole array of other
properties a surface might have that one might notice while trying to describe
it.
. In fact, we computed Euler numbers
ad delectam.
Why did we do this? One reason
is that they are is easy to compute. But that is not obviously a compelling
reason for doing anything in mathematics. The real reason is that it
is an invariant of the surface (it does not depend upon what map one puts
on the surface) and because it is connected to a whole array of other
properties a surface might have that one might notice while trying to describe
it.
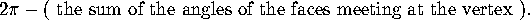

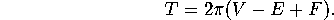
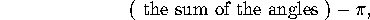

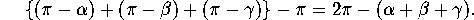
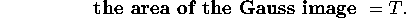
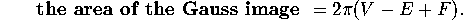
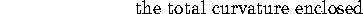
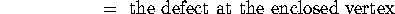
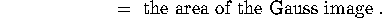
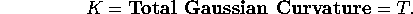
 . But the conceptual idea is still the same. Any curved surface can be approximated by a polyhedral one with lots and
lots of vertices. The curvature of the surface within a path (a smooth
piece of peel) is then very nearly equal to the sum of the defects
at all the encircled vertices. By a technical limiting argument that
involves integrals to give a precise meaning to curvature,
. But the conceptual idea is still the same. Any curved surface can be approximated by a polyhedral one with lots and
lots of vertices. The curvature of the surface within a path (a smooth
piece of peel) is then very nearly equal to the sum of the defects
at all the encircled vertices. By a technical limiting argument that
involves integrals to give a precise meaning to curvature,