 indicates the addition of a handle;
a final circle
indicates the addition of a handle;
a final circle  the addition of a cross cap.
the addition of a cross cap.
A symmetry group is the collection of all symmetry operations of a pattern. We give the same names to symmetry groups as to the corresponding quotient orbifolds.
We regard every orbifold as obtained from a sphere by adding cone-points,
mirror boundaries,
handles, and cross-caps.
The major part of the notation enumerates
the orders of the distinct cone points,
and then the types of all the different mirror boundaries.
An initial black spot  indicates the addition of a handle;
a final circle
indicates the addition of a handle;
a final circle  the addition of a cross cap.
the addition of a cross cap.
For example, our brick wall gives 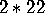 ,
corresponding to its gyration point of order 2,
and its mirror string with two 2-way corners.
,
corresponding to its gyration point of order 2,
and its mirror string with two 2-way corners.
Here are the types of some of the patterns shown in section 31:
Figure 14:  ;
Figure 15:
;
Figure 15: 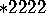 ;
Figure 16:
;
Figure 16: 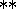 ;
Figure 17:
;
Figure 17: 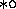 .
Figure 18:
.
Figure 18: 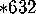 .
Figure 19:
.
Figure 19: 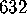 .
.
Appart from the spots and circles, these can be read directly
from the pictures: The important thing to remember is that if
two things are equivalent by a symmetry, then you only record
one of them.
A dodecahedron is very like a sphere.
The orbifold corresponding to its symmetry group is a
spherical triangle having angles 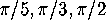 ;
so its symmetry group is
;
so its symmetry group is 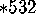 .
.
You, the topologically spherical reader,
approximately have symmetry group  ,
because the quotient orbifold of a sphere by a single reflection
is a hemisphere whose mirror boundary has no corners.
,
because the quotient orbifold of a sphere by a single reflection
is a hemisphere whose mirror boundary has no corners.