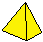


 4
4 

 4
4 

 4
4 



 4
4  6
6 

 4
4  6
6 
| F = # of faces E = # of edges V = # of vertices |
| Model | F | E | V | Shapes |
| Tetrahedron | ||||

| 4 | 6 | 4 | 4  |
| Truncated Tetrahedron | ||||

| 8 | 18 | 12 | 4  4 4  |
| Octahedron (Tetratetrahedron)* | ||||

| 8 | 12 | 6 | 4  4 4  |
| Truncated Tetrahedron | ||||

| 8 | 18 | 12 | 4  4 4  |
| Tetrahedron | ||||

| 4 | 6 | 4 | 4  |
| Cuboctahedron (Rhombitetratetrahedron)* | ||||

| 14 | 24 | 12 | 4  4 4  6 6  |
| Truncated Octahedron (Rhombitruncated tetratetrahedron)* | ||||

| 14 | 36 | 24 | 4  4 4  6 6  |
*The names in the parenthesis will be explore further in Lesson 12: Naming Polyhedra
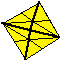
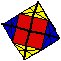
We have picked tetrahedron and rhombitetratetrahedron to show the 2-, 3-, and 3- fold symmetries in this group. In each of the polyhedra below, we have highlighted some planes of reflection symmetry to show the folds of symmetry.
| 2-fold | 3-fold | a different 3-fold |
| 
|  |
| 
|  |