NAMING POLYHEDRA
ACTIVITY SHEET
The exercises contained in this activity require the KaleidoTile
program developed by Jeff Weeks. If you do not yet have a copy of this
software, you may wish to
download KaleidoTile
.
For more information regarding this activity and its objectives, see the
accompanying Teacher's Guide.
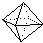
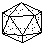
1. Get models of the five Platonic solids to study. Each Greek
prefix in the table below represents a number. Name each Platonic solid
shown in the lower table by:
2. Look at the sketches of polyhedra that you made from the Intro.
to KaleidoTile lesson. Check the names you gave to the Platonic
solids above with the names given to your sketches from
KaleidoTile. Are any of the names different?
If so, explain why.
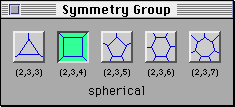
3. Load the KaleidoTile program on your computer. You will study one
polyhedra family, called the (2,3,4)-family. To do so, choose the
settings shown here:
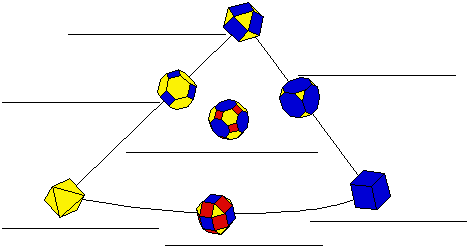
- In the Basepoint window, drag the base point to each vertex
dot and write the name of the polyhedron formed in the (2,3,4) -Family
Diagram.
(2,3,4)-Family Diagram
- Starting with the base point at the lower right vertex dot, slowly
drag the base point along the right edge of the base triangle triangle
until you reach the dot in the middle of the edge. Watch as the cube
transforms into a new polyhedron. Describe how the polyhedra are
changing.
- Continue to drag the base point along the right edge of the base
triangle until you reach the upper vertex dot. Again describe how the
polyhedra are changing.
- Place your base point at the lower left vertex dot. Slowly drag the
base point along the left edge of the base. Describe what happened to the
Platonic solid as you moved the base point away.
- Give your own definition of the word truncated.
- Notice that the name of the polyhedron at the top vertex dot is a
combination of the names of the two Platonic solids in lower vertices.
Why do you think that is?
- Starting at the top vertex, slowly drag the base point straight down
toward the dot in the center of the triangle. You are truncating
the polyhedron. Pause when you reach the center dot. Then continue
until you reach the dot in the middle of the lower edge. Note that these
last two polyhedra names have rhombi in them. What do you think
rhombi means?
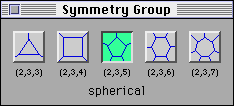 4. It's time to check what you learned by studying a different family of
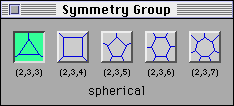
polyhedra, the (2,3,5)-family. Change the Symmetry Group by
pressing the (2,3,5) button.
4. It's time to check what you learned by studying a different family of
polyhedra, the (2,3,5)-family. Change the Symmetry Group by
pressing the (2,3,5) button.
- Fill out the (2,3,5)-Family Diagram below by dragging the base point
to each vertex dot.
(2,3,5)-Family Diagram
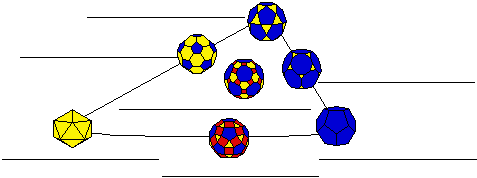
- Once again, starting with the base point at the lower right vertex
dot, slowly drag the base point along the right edge of the base triangle
triangle. Similarly, start at the lower left vertex dot and drag the
base point along the left edge. What word describes what is happening in
both cases?
- Starting at the top vertex, slowly drag the base point straight down
toward the dot in the center of the triangle. Pause when you reach the
center dot. Then continue until you reach the dot in the middle of the
lower edge. What shapes do these last two polyhedra have that give them
rhombi in their name?
- Explain what rhombitruncated icosadodecahedron means.
5. Let's see if you know what is really going on.
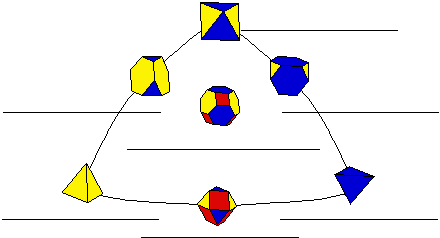
- Two names of the (2,3,3)-family are given in the diagram below.
Use what you learned from studying the (2,3,4)- and (2,3,5)-families to
fill in the other five names. Do NOT use KaleidoTile for this!
It will give you incorrect names.
(2,3,3)-Family Diagram
- KaleidoTile gives some different names than you should have
written. Change the Symmetry Group by pressing the (2,3,3)
button. Fill out the (2,3,3)-Family Diagram below, this time using
KaleidoTile.
(2,3,3)-Family Diagram

- Explain why KaleidoTile named these polyhedra differently
than it did for the first two families.
| MAIN | NEXT ACTIVITY |
POLYHEDRA CHARTS |
Copyright © 1995 by
The Geometry Center,
all rights reserved.

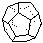



 4. It's time to check what you learned by studying a different family of
polyhedra, the (2,3,5)-family. Change the Symmetry Group by
pressing the (2,3,5) button.
4. It's time to check what you learned by studying a different family of
polyhedra, the (2,3,5)-family. Change the Symmetry Group by
pressing the (2,3,5) button.


