Next: Inversion
Up: Peaucellier's Linkage Table of Contents
Prev: Introduction

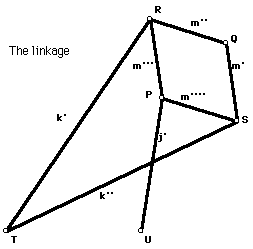
Peaucellier's Linkage

Part 1. Construct the Linkage

Construct the linkage as follows. Once you have a sketch, make this procedure into a script.

1. Start with three segments off to the side which determine your three lengths; label them j, k, and m.
2. Construct your two "fixed" points T and U so that the distance between them is the same as the length of j.
3. Now construct P so that the distance from P to U equals that from T to U and so that P is free to move around U.
4. How do you determine the placement of R and S? Remember that they are both a specified distance (the length of k) from T and a specified distance (m) from P. Construct them.
5. To determine the placement of Q, use the fact that PRQS must be a rhombus. You could construct Q using either intersections of parallel lines or intersections of circles. For technical reasons, intersections of parallel lines works better. Construct Q.
6. After completing your sketch, move P while you trace P and Q to form conjectures as to the shapes their traces lie on.
7. Change the lengths of the three segment and move P while you trace P and Q again. Does your conjecture remain true?

By now you have formulated a conjecture for the shape traced by Q as P moves. The next question is: Why do P and Q behave as they do? In the next section, you will learn about inversion. In part 3, you apply this knowledge to your linkage to understand why P and Q move as they do.

Introduction

---

Author: Evelyn Sander
Comments to: webmaster@geom.umn.edu
Created: Jun 09 1996 --- Last modified: Jun 11 1996