A linkage is a series of straight rods connected at the ends, which are free to pivot in a plane. You can construct a physical version of such an object. For example, you can make one out of parts from an erector set or even popsicle sticks. We are going to study a particular linkage originally constructed by Peaucellier.


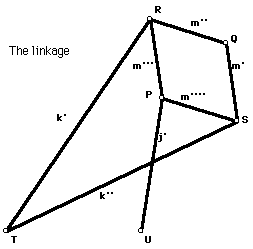
Peaucellier's linkage consists of two fixed points at a specified distance from each other, marked T and U in the figure, and seven rigid rods of specified size, attached together as indicated in the picture. Aside from the following constraints, the rods are free to move.
Constraints: As you see, rods are: PU, PS, QS, QR, PR, TR, and TS. The specified sizes are: Distance from T to U=PU, PS=QS=QR=PR, and TS=TR.
Notice that of the seven segments, four are one length, two the next, and one a third length, the last one being also the distance between the two fixed points. Do the assumptions about how they are attached give any additional information about the three possible lengths?
You will construct the linkage of Peaucellier and study it. Before you begin, consider the following questions. The first question, you should be able to reason out. The second question is the topic you will study for the rest of the lab.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Evelyn Sander
Comments to:
webmaster@geom.umn.edu
Created: Jun 09 1996 ---
Last modified: Tue Apr 15 15:14:01 1997