An orbifold is a sort of "fractional manifold", and the orbifold Euler characteristic may take fractional values, even though it is still defined as V-E+F.
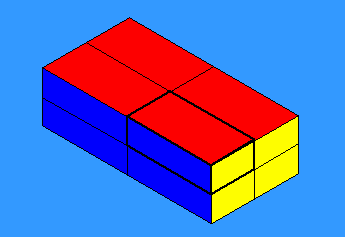
Let's take as an example the map obtained from a brick by dividing each face into four rectangles. This has V=26, E=48, and F=24 , so indeed V-E+F=2: the Euler characteristic of a sphere. Since the symmetry group of the brick has order eight, its orbifold comes from one eighth of the surface of the celestial sphere, and the calculation of its orbifold Euler characteristic should yield one eighth of the Euler characteristic of the sphere. Let's see how this comes about.

Indeed, the orbifold (or base triangle) has 3=24/8 faces. But the number of edges seems to be 9 (three edges meet at the corner of the brick and six edges run around the boundary of the orbifold), rather than 48/8=6. What's wrong?
The answer is that the "six edges" on the boundary are really only half-edges, because each of them is shared equally between two copies of the orbifold! So for the orbifold, E is really
1 + 1 + 1 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 = 6.
In a similar way, there is one full vertex (lying in only one copy of the orbifold), three half-vertices (shared between two copies), and three quarter-vertices (each lying in four copies of the orbifold), so that
V = 1 + 1/2 + 1/2 + 1/2 + 1/4 + 1/4 = 3 1/4,
which is indeed 26/8.
The same thing happens for all orbifolds obtained from the sphere! Any map on the orbifold comes from a map on the sphere by "dividing" by some group of order N, say. If the map on the sphere has
V vertices, E edges, F faces,
then with our conventions, the map on the orbifold will have
V/N vertices, E/N edges, F/N faces,
and so its orbifold Euler characteristic will be:
(V-E+F)/N = 2/N.
The Orbifold euler characteristic of a spherical pattern is just the Euler characteristic of the sphere divided by the order of the symmetry group of the pattern. In particular, since the Euler characteristic for the sphere is independent of the particular map on it, the same is true for the orbifold Euler characteristic. This means that we can choose the map to suit our needs and not worry about changing the results of our calculation.
We can now use our idea of fractional vertices, edges, and faces to compute the costs of the features of an orbifold.
Gyration points. (n)
The cost of replacing an ordinary point by a 4-fold gyration point can be found by making that point be a vertex of some map. Before the change, this counts as a full vertex; after it, only as a quarter of a vertex. So the change reduces the Euler characteristic by
1 - 1/4 = 3/4.
In general, the cost of an n-fold gyration point is (n-1)/n.
Mirror boundaries. (*)
When we add a new mirror boundary (with no corners), we are really punching a hole in the orbifold. If we take this hole to be a face of some map on the original orbifold, we see that the change reduces the characteristic by 1, since it removes one face and halves all the edges and vertices around the hole.
Mirror corners. (n after a *)
Let's change an ordinary boundary point into an order 2 corner point by taking the point concerned to be a vertex of our map. Before the change, it is really a half-vertex, since there is only 180 degrees of surface around it. After the change, it becomes a quarter- vertex (90 degrees). The change reduces the characteristic by
1/2 - 1/4 = 1/4.
If we had changed it instead to an order n corner point, the cost would have been 1/2 - 1/(2n) = (n-1)/(2n). Doing things with mirrors costs exactly half as much as doing them without, because a mirror divides everything by 2.
Handles and cross caps (o and x)
We quote from the topology books the fact that every unbounded compact 2-manifold can be obtained from a sphere by adding either handles (o in Conway's notation) or cross caps (x). Each handle reduces the characteristic by 2, and each cross cap reduces it by 1.
Since each orbifold is a manifold with holes (mirrors) cut in it and points (corners and cones) put on, we can obtain all 2-dimensional orbifolds by first adding holes, handles, and cross caps to a sphere, then adding corners and cone points to the resulting manifold. The most general orbifold symbol consists of a number of circles followed by a number of digits, then expressions such as *abc... and maybe some crosses.
Our arguments show that if we start with $2 and "buy" our orbifold, the change we'll get is $2/n, where n is the group order (we'll go home flat broke if our group was one of the seventeen infinite crystallographic groups in the flat Euclidean plane). In other words, if something has n symmetries, its orbifold Euler characteristic is 2/n. Let's check this on a few examples.

The running bond brick wall (see the examples page) has symbol 2*22; therefore its cost is:
1/2 + 1 + 1/4 + 1/4 = 2.
The half sailor brick wall's orbifold with symbol *2222 similarly costs:
1 + 1/4 + 1/4 + 1/4 + 1/4 = 2.
In each case, we started with $2 and ended up flat broke; therefore the symmetry group acts on the flat plane. These have 0=2/(infinity) for their orbifold Euler characteristic, so they have infinitely many symmetries.
Our rectangular table had symmetry group *22. This costs:
1 + 1/4 + 1/4 = 3/2.
The change is 1/2, or 1/4 of the money we started with. This is because the mirror lines cut the sphere into 4 slices. Our initial capital of $2 has been divided by 4 because 4 is the number of slices the symmetries of the table cut the sphere into. (The same as the number of pieces of orange peel left when you finished the extra credit project.) This is equal to the number of elements of the symmetry group of the table.
When we do the same thing with the chair, we get $1 in change, which means 1/2 of our money is left at the end. Thus, the symmetry group of the chair has order two. This group consists of the identity element (which leaves the chair alone) and the mirror reflection which reflects the chair down its middle.
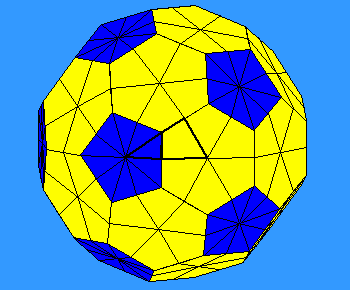
The soccer ball has symbol *532, and so has cost
1 + 4/10 + 2/6 + 1/4 = 119/60.
Hence we have an orbifold Euler characteristic (or change from $2) of $1/60, or 1/120 of what we started with. So the symmetry group of the soccer ball has order 120, and the orbifold covers one one hundred and twentieth of the surface of the sphere.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Heidi Burgiel
Comments to:
webmaster@geom.umn.edu
Created: Dec 7 1995 ---
Last modified: Jun 11 1996
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.