_ _ _ _ _ _ _ _ | | | | | | | | | (vertical bricks) |_|_|_|_|_|_|_|_|_ _|___|___|___|___| (horizontal bricks) | | | | | | | | | (vertical bricks) |_|_|_|_|_|_|_|_|_ _|___|___|___|___| (horizontal bricks) | | | | | | | | | |_|_|_|_|_|_|_|_| (vertical bricks)
In this pattern there are four different lines of mirror symmetry. Two of these run vertically through the centers of the vertical bricks (just one of them also runs through the centers of some horizontal bricks), and two run horizontally through the centers of the bricks in a row. Our mirror string is rectangular.
_________ | # | | # | | # | | # | | # | ######### # | #_______|
It has corners of four different types: running round it we find four 2-way kaleidoscopic points; one in the center of a vertical brick, one in the center of a horizontal brick, one in the mortar between two horizontal bricks, and one vertically above that one in the center of a another vertical brick. The type of this mirror string is *2222. There is no gyration point, so *2222 is also the orbifold notation for the discopic symmetry group of this tiling. Note that this is another discopic group; because it has no gyration points we can refer to this as "the" discopic symmetry group of the plane.
When we fold the pattern along its mirror lines, we get the rectangle shown above. Since there are no symmetries of the pattern other than the mirror symmetries, the rectangle shown is the orbifold of the half sailor pattern.
___ _ _ ___ |___| | |___| (horizontal, vertical, vertical, horizontal) |___|_|_|___| | | |___| | | (vertical, vertical, horizontal, vertical, vertical) |_|_|___|_|_| |___| | |___| (horizontal, vertical, vertical, horizontal) |___|_|_|___|
This brick pattern (called "basket weave bond") has a square mirror string enclosing four half bricks, a pinwheel of mortar, and a gyration point. A rotation through one quarter of a revolution about this gyration point does not change the pattern. This shows that the four 2-way mirror points at the corners are equivalent, so this mirror string has type *2 (NOT *2222 or *22), and the orbifold notation for this group is 4*2. The digit 4 represents the central gyration point, and the group is called "tetragyros" (short for tetragyrodiscopic).
____
#####- #
| # #
| # #
|#########|
# # |
# # |
#_____#####
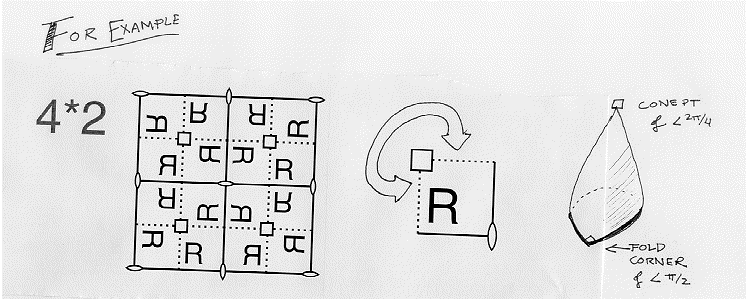
4*2

To construct the orbifold we fold the surface along mirror lines until we get this square region, then slit from the edge of the square to the central gyration point. We can then wrap the square up to get a four layered cone, like an ice cream cone with one right angled corner (or like a gyro sandwich made from a square pita). Our orbifold has an order 4 cone point and a mirror boundary with one right angled corner; it is also denoted 4*2.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Heidi Burgiel
Comments to:
webmaster@geom.umn.edu
Created: Dec 7 1995 ---
Last modified: Jun 11 1996
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.