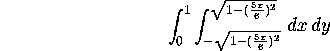Convergence of Riemann Sums

where D is the ellipse with axes 6/5 and 1. This is equivalent to the double iterated integral

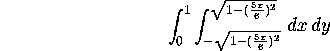
According to the theory of Riemann sums (discussed in class) this integral should equal the limit of the area of our approximation as the grid gets finer and finer.

Question #5

• Use the leftbox2d command to approximate the area of the ellipse for several grid sizes. For example you might want to use:
  • grid=[10,10]
  • grid=[12,12]
  • grid=[15,15]
  • grid=[20,20]
  • grid=[25,25]
• Plot the approximate area versus the total number of boxes in your grid.
• Indicate the true value of the area of the ellipse on your graph. Would you say that the approximate areas are converging quickly or slowly to the actual area? Do the approximations increase monotonically towards the actual area? Explain why you think the graph looks like it does.
• Based on your graph, try to estimate how many rectangles we'd need in a square grid in order to
  • approximate the area to within 0.05 of the true area AND
  • ensure that if we refine the grid (that is, increase the number of rectangles) then the new approximate area will remain within 0.05 of the true area.
  How confident are you in your answer? (You may want to compute approximations for more grid sizes.)