A Triangle Exploration
In this activity, you will look at the relationship between the measurements of the sides of a triangle and the measurements of its angles.
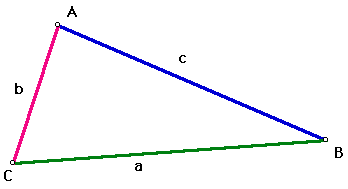
Click
here
or on the picture to go to an interactive sketch for this activity.
Use the pointer tool to grab a vertex of the triangle and change the length of a side. For this exercise, you will want to keep side c as the longest side of the triangle.
While you are changing the lengths of the sides of the triangle, keep your eye on the following things:
- The measures of angles A, B, and C
- The value of a^2 + b^2
- The value of c^2
If you would like to use a more detailed interactive sketch that shows the squares of the sides of the triangles as areas, 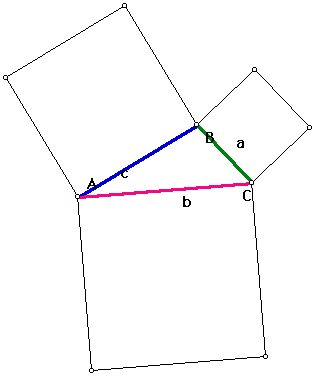
click here
or on the picture.
Questions to consider:
Are there times when you notice a relationship between the squares of the two legs of the triangle and the square of the hypotenuse? Drag the vertices of your triangle so that the relationship exists. Now look at the measures of angles A, B, and C. Is there anything special about the angles? Find a different triangle that satisfies the relationship with the squares of the legs and the hypotenuse. Take a look at the angle measures of this triangle. How do they compare to the measures of the angles of the previous triangle? Are you ready to make a conjecture about the squares of the legs and hypotenuse of the triangle and the measure of its angles? If so, test out your conjecture on some more triangles. If you're not ready, take a look at some more triangles and see if you can find a pattern.
After you have tested your conjecture...
The ancient Egyptians and Babylonians knew of a relationship that occurred between the sides and angles of certain triangles. Click here to see if you have realized the same thing.
 Return to Main Menu
Return to Main Menu


