Centers of Mass and Centroids
Two Point-Masses
Suppose we have two particles of mass m1 and m2 at
positions x1 and x2 , and suppose that the particles
are connected by a lightweight inflexible rod. We say the
particles form a system or a rigid body. Analyzing the properties of
such a system is the first step to understanding the properties of
more complicated objects.
One of the most important properties of the system is the center of
mass . Intuitively, the center of mass
is the location where an object could balance
perfectly level on the tip of a pin.

Figure 1: An asymmetric dumbell-shaped object.
Group Discussion
Describe the center of mass for the two particle system if
- m1 = m2
- m1 > m2
- m1 = 2 m2
The center of mass of an object is also the position at
which the entire mass of the object could be concentrated, and still
have the same "average motion" as the entire object does.
The center of mass is vital to
understanding the dynamics of a system of particles. For example, if
we throw the "dumbell" shown in Figure 1, then the center of mass will
follow a fairly simple path (roughly parabolic) whereas the ends will rotate around the center of mass,
creating complicated paths as shown in Figure 2.
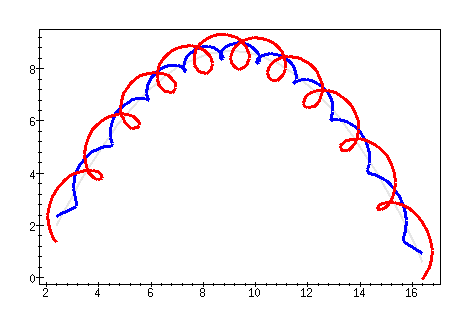
Figure 2: The motion of a rotating dumbell-shaped object.
Many Point-Masses
Suppose a rigid body is composed of n particles connected in a
straight line. If the i th particle is located at
x_i and has mass m_i , then the location of the
center of mass for the system is x_cm where
(m1 + m2 + . . . + m_n)x_cm = m1 x1 + . . . + m_n x_n
The derivation of this equation involves
finding the "pivot point" where the torques induced by the weight of each
particle cancel out.
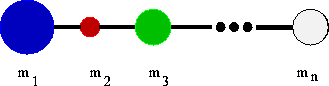
Figure 3: A rigid collection of n particles.
Note that this equation indicates why
the rigid body "acts like" a point mass located at the
center of mass. If we imagine trying to balance the whole system on a
pivot located at the origin, each individual mass exerts a torque of
m_i x_i . The net torque at the origin is then just the
sum of the individual torques, which is the right hand side of the
equation above. On the other hand, the torque exerted by a single
particle of mass m_1 + ... + m_n located at x_cm
is given by the left hand side of the equation.
If the particles are positioned
in the plane at coordinates (x1,y1), ..., (x_n, y_n) , then the coordinates of the center of
mass are defined by (x_cm , y_cm ) where
(m1 + . . . + m_n) x_cm = m1 x1 + . . . + m_n x_n
(m1 + . . . + m_n) y_cm = m1 y1 + . . . + m_n y_n
Question 1
When the shape of an object is symmetric, it is clear where the center
of mass is. We can often use this observation to find the
centers of mass for composite objects by decomposing them into
symmetric regions that we can then treat as point masses.
Answer the following questions by interacting with the
Exploring Centers of Mass page.
- Experimentally find the center of mass for the "C-beam" cross-section
(also called a "channel section" by engineers) on the next page.
You'll know you are essentially correct when the background color turns
yellow.
- Decompose the C-beam into a union of rectangles by selecting
one of the "Simple Subdivisions" from the menu at the bottom of the
Exploration page, and find the center of mass for
this subdivision. (Notice the black dots at the center of mass for
each rectangle.) Does the center of mass of the
C-beam change as the subdivision changes? Why does this make sense?
- If we can decompose a composite region into simple symmetric regions, then
the center of mass of the composite region may be found by
replacing each simple region by a corresponding point-mass.
- Give a geometric argument for why the statement should be true.
What should be the location of each point-mass?
What should be the mass of each point-mass?
- Verify the statement above using the C-beam with "Simple
Subdivision 1" as a concrete example.
In particular, assume that the "legs" of the C-beam
have width 0.62 and height 2.17, and the "roof"
has width 4.34 and height 0.62. Assume the C-beam has
constant density of 1. Determine both the
location and mass of the three point-masses
inside the "Simple Subdivision 1" on the Exploration page.
- As this example shows, the center of mass of an object does not need to
be on the object, yet it still makes sense to say that the center of mass
is the location where the center of mass would balance on your finger
and be perfectly level. Explain how a physical model of
the C-beam can be made to balance
at its center of mass. (Hint: consider
line segments that connect the center of mass of the C-beam
to the center of mass of each rectangle in the C-beam's
decomposition.)
Next: Centers of Mass for Continuous Objects
Return to: Outline
The Geometry Center Calculus Development Team
Copyright © 1996 by The Geometry Center.
Last modified: Fri Apr 12 15:41:19 1996


