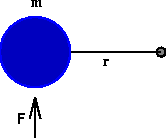

The tendency of the particle to rotate around the pivot depends on the force F perpendicular to the connecting rod applied to the particle, and the distance r to the pivot . We define the torque T by the formula
T = F r
The greater the force or the greater the distance from the pivot, the larger the torque, and hence the greater the tendency to rotate.
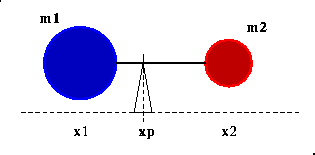
If we try to balance the system on a pivot at a point x_p in between x_1 and x_2 , both particles exert torques that tend to tip the beam, rotating it around the pivot. In order to balance the system on the pivot, we want the torques caused by each of the particles to cancel each other. Since the force exerted by each particle is given by its mass times the acceleration of gravity, x_p must be chosen so that
m_1 g (x_1 - x_p ) = m_2 g (x_2 - x_p )
Rearranging this equation gives
x_p (m_1 + m_2 ) = (x_1 m_1 + x_2 m_2 )
This line of reasoning easily generalizes. If a rigid body is composed of n particles connected in a straight line, then the location of the center of mass for the system is x_cm where
(m1 + m2 + . . . + m_n)x_cm = m1 x1 + . . . + m_n x_n
Copyright © 1996 by The Geometry Center. Last modified: Fri Apr 12 15:46:55 1996