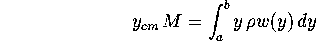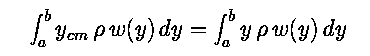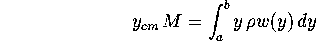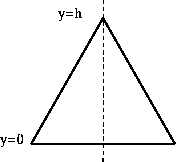Centers of Mass for Continuous Objects
For objects that are not symmetrical, we can find the center of mass
by using the techniques of integral calculus. We cut the object into
many small pieces and treat each of them as a point mass. The center
of mass of the resulting system is approximately the same as the
center of mass of the continuous object. As the number of pieces grows
and their sizes shrink, the limit of the approximate solution
approaches the true center of mass.
In practical terms, the summations turn into integrals. We want to
think of the object as being cut into thin strips of small mass. For
example, in Figure 4, the object is horizontally symmetric, so
x_cm = 0 .
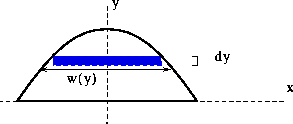
Figure 4: Slicing an irregular object into strips.
To find y_cm , we can chop the object into strips
of small mass: dm = p w(y) dy , where p is the
density of the object. Then y_cm satisfies
the equation
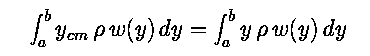
where a is the minimum value of y
and b is the maximum value of y .
Observe that this formula doesn't seem to involve the mass of the
object, only its shape. However, since y_cm is a constant,
we can integrate the left hand side of the equation. Since
the integral of the density over the region is the mass of the object, we have
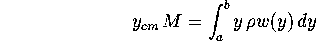
where M is the total mass of the object.
For this lab, we will always assume that our objects have uniform
density. To make it clear that we are making this assumption, we call
the point (x_cm, y_cm) defined by the above integral
formula the centroid instead of the center of mass. Another
way to think about it is that the centroid would be the center of mass
if the object were cut out of a mathematically perfect, uniform
material.
Question 2
- Find the centroid of an isosceles triangle
with height h and base length B .
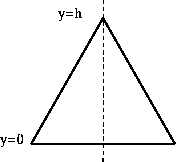
- A trapezoid of height h has a bottom edge of length
2B and a top edge of length B and is
symmetric with respect to the y -axis. Use
the answer to the previous problem and your experience with Question 1
to compute the centroid for this trapezoid.
Next: Moments of Inertia
Return to: Outline
The Geometry Center Calculus Development Team
Copyright © 1996 by The Geometry Center.
Last modified: Fri Apr 12 15:43:41 1996