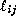 of the edge
connecting nodes
of the edge
connecting nodes 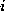 and
and 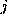 should be
should be
The graph can be easily laid out in the hyperbolic plane using
uniform edge lengths. Indeed, this property of hyperbolic geometry is
one of the motivations behind its use. However, we would like to
optimize our use of space so that as many generations as possible are
visible. (This optimization also forestalls a bit longer the
inevitable cumulative floating-point error). So we would like edges
that connect nodes to be as short as possible, yet we must also avoid
overlaps between the cone trees of all
future generations. In order to most economically meet these
constraints, the hyperbolic length 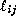 of the edge
connecting nodes
of the edge
connecting nodes 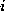 and
and 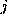 should be
should be
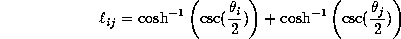
where 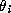 denotes the smallest angle between edges incident
on node
denotes the smallest angle between edges incident
on node 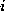 (see Figure 5).
(see Figure 5).
When the cone tree angle (a user-specifiable parameter) is 90 degrees, cones become flat disks. While this would negate most of the advantages of cone trees in Euclidean space, in hyperbolic space disks are very convenient. The hierarchy of disks has no directional bias: locally, child nodes are indistinguishable from parent nodes. Whichever node is closest to the origin of the sphere ``feels'' like the root node.
Figure 5: Angle between edges incident on node i.