Mathematically consistent alternatives to Euclidean geometry have been developed over the past hundred years. The noneuclidean geometries can be distinguished by the behavior of parallel lines: in Euclidean space there is exactly one line passing through a given point which is parallel to a given line, but in hyperbolic geometry there are many. In this space the area of a circle grows exponentially with respect to its radius, whereas in Euclidean space the area only grows linearly. Thanks to this property of hyperbolic distance we have a convenient way to visualize exponentially growing trees.
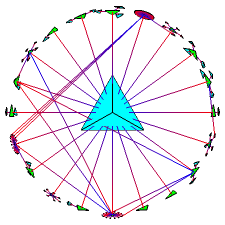
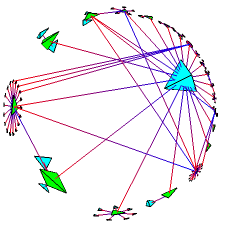
The simplest way to draw 3D hyperbolic pictures is in the interior of a ball. We use Euclidean straight lines, but the way we measure distance is changed so that the surface of the ball is infinitely far away from the origin. From the outside, objects very near the center seem almost Euclidean but seem to grow distorted and smaller as they are translated towards the surface of the ball. This representation of hyperbolic space is known as the projective or Klein model. Luckily we can draw such pictures using 4 x 4 matrices: since the standard graphics pipeline uses homogeneous coordinates, interactive speeds are easily achieved on modern workstations. Figure 3 shows a navigation sequence in the projective model. The look and feel of the system is difficult to communicate with still pictures, a video is necessary to do it justice.
Figure 3: Motion in hyperbolic space (the projective model)
WebOOGL [120 KB] VRML [250 KB] MPEG [900 KB]
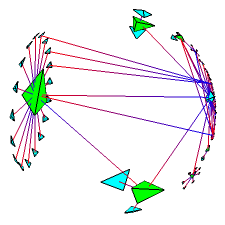
The conformal or Poincaré model is related to the projective model by a simple transformation. In this model, straight lines are drawn as arcs and flat faces are drawn as parts of spheres. The advantage is that angles are always drawn correctly. Unfortunately we cannot use 4 x 4 matrices to represent motion in the conformal model, and drawing arcs and curved faces also requires much greater subdivision than in the projective case. While this model is more computationally demanding than the projective one, it is within the reach of most workstations.
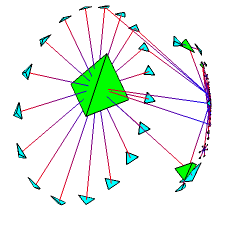
If we allow the camera to go outside of the ball we can see the
entire space at once. When we constrain the camera itself according to
hyperbolic isometries, it can never move outside of the ball and we
see what hyperbolic space would look like from the insider's point of
view. These three models provide different and useful intuition, so we
use whichever of them is appropriate at any given time. Figure
4 shows two levels of the Geometry Center
Weblet in the three models. (We use ``Weblet'' to refer to a section
of the Web ![]() .) Here we have drawn the ``sphere at infinity''
for the two outsider models but in all other pictures the sphere is
not shown.
.) Here we have drawn the ``sphere at infinity''
for the two outsider models but in all other pictures the sphere is
not shown.
Figure 4: The projective, conformal, and ``insider'' models of hyperbolic space
MPEG projective [1.15MB] MPEG conformal [700KB] MPEG insider [360KB]
There has been considerable work at the Geometry Center on visualizing hyperbolic geometry. The 1991 mathematical animation Not Knot [3] includes a groundbreaking flythrough of hyperbolic space. A reference on hyperbolic navigation can be found in [1], which to the best of our knowledge contains the first recorded suggestion of using hyperbolic space for tree visualization. See also [2] for more exposition of hyperbolic geometry aimed at the computer graphics community.
The publicly distributed Geomview 3D viewer [8] includes built-in support for interactive navigation in noneuclidean geometries, including hyperbolic geometry. Details on the implementation of the hyperbolic transformation libraries used in Geomview can be found in [7].
A recent paper from Lamping et al at Xerox PARC [4] has brought hyperbolic visualization to the attention of the computer-human interaction community. They ran user tests of a 2D Poincaré model browser visualizing various kinds of hierarchical information, including organizational charts and a Weblet. Their work on information visualization is confined to the 2D hyperbolic plane, and deals only with acyclic graphs.
Hyperbolic space has a similar visual effect to a fisheye camera lens, used by [10] for information visualization. The fisheye paradigm calls for several ad-hoc decisions, the advantage of hyperbolic geometry is it provides an elegant and powerful mathematical framework for display and navigation.