![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
We consider a discrete dynamical system
given by a diffeomorphism on 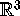 . Such a map may be given explicitly,
or be obtained as the Poincaré map of a vector field on a four-dimensional
state space.
Stable and unstable manifolds of invariant manifolds of saddle-type,
here fixed points or invariant circles,
play important roles in organizing the
global dynamics. It is well-known that
the stable manifolds
form boundaries between different basins of attraction.
Furthermore, the transverse intersection of stable
and unstable manifolds leads
to homoclinic or heteroclinic tangle, associated with chaos.
These manifolds are global,
often noncompact objects that can have very
complicated structure.
Only in special situations it is possible to find
stable and unstable manifolds analytically. In general
they need to be computed
with numerical methods.
. Such a map may be given explicitly,
or be obtained as the Poincaré map of a vector field on a four-dimensional
state space.
Stable and unstable manifolds of invariant manifolds of saddle-type,
here fixed points or invariant circles,
play important roles in organizing the
global dynamics. It is well-known that
the stable manifolds
form boundaries between different basins of attraction.
Furthermore, the transverse intersection of stable
and unstable manifolds leads
to homoclinic or heteroclinic tangle, associated with chaos.
These manifolds are global,
often noncompact objects that can have very
complicated structure.
Only in special situations it is possible to find
stable and unstable manifolds analytically. In general
they need to be computed
with numerical methods.
In this paper we compute the two-dimensional
unstable manifold 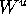 of an invariant manifold of saddle-type
of a three-dimensional diffeomorphism.
(The stable manifold
can be computed by considering the inverse.)
There are two different cases: the unstable manifold
of an invariant manifold of saddle-type
of a three-dimensional diffeomorphism.
(The stable manifold
can be computed by considering the inverse.)
There are two different cases: the unstable manifold 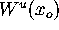 of a hyperbolic fixed point
of a hyperbolic fixed point
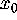 , and the unstable manifold
, and the unstable manifold 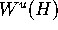 of a normally hyperbolic
invariant circle H.
The Unstable Manifold Theorem
[Hirsch et al. 1977,
Palis and De Melo 1982]
guarantees the existence of
the local unstable manifold
of a normally hyperbolic
invariant circle H.
The Unstable Manifold Theorem
[Hirsch et al. 1977,
Palis and De Melo 1982]
guarantees the existence of
the local unstable manifold
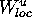 in a neighborhood of the invariant
manifold of saddle-type. The two cases are sketched in
Figure 1. See also the
animations.
in a neighborhood of the invariant
manifold of saddle-type. The two cases are sketched in
Figure 1. See also the
animations.
The idea is to obtain the global unstable manifold 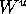 by globalizing the
local unstable manifold
by globalizing the
local unstable manifold 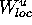 .
In practice, we
reliably compute a sufficient piece of
.
In practice, we
reliably compute a sufficient piece of 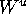 ,
so that conclusions on the global dynamics can
be drawn.
The unstable manifold
is represented by a discrete set of mesh points.
The quality of the mesh can be
prescribed, and the mesh is adapted whenever necessary.
Our algorithm was originally
developed for the computation of unstable manifolds
of a normally hyperbolic invariant
circle of saddle-type. With a slight adaptation,
it can also be used to find a two-dimensional unstable
manifold of a hyperbolic
fixed point.
,
so that conclusions on the global dynamics can
be drawn.
The unstable manifold
is represented by a discrete set of mesh points.
The quality of the mesh can be
prescribed, and the mesh is adapted whenever necessary.
Our algorithm was originally
developed for the computation of unstable manifolds
of a normally hyperbolic invariant
circle of saddle-type. With a slight adaptation,
it can also be used to find a two-dimensional unstable
manifold of a hyperbolic
fixed point.
As starting data for our algorithm we need an approximation
of the local unstable manifold 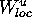 .
There are different algorithms
for computing
.
There are different algorithms
for computing 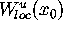 of a hyperbolic fixed
point
of a hyperbolic fixed
point 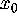 ;
see [Osinga 1996] and biblio therein.
The work presented here was motivated
by the possibility of
obtaining the starting data for the
computation of the unstable manifold
;
see [Osinga 1996] and biblio therein.
The work presented here was motivated
by the possibility of
obtaining the starting data for the
computation of the unstable manifold 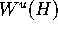 of an
invariant circle H of saddle-type
in the form of a
linear approximation of
of an
invariant circle H of saddle-type
in the form of a
linear approximation of 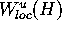 with the method in
[Osinga 1996,
Broer et al. 1996,
Broer et al. 1997]. Their method is a variation of the graph
transform that allows the computation
of a normally hyperbolic
invariant circle of saddle-type of a three-dimensional map.
The key idea is to start with a known invariant circle H of
a map f together with the Df-invariant splitting of the tangent
space at H. This splitting induces Df-invariant stable and
unstable normal bundles that are embedded in
with the method in
[Osinga 1996,
Broer et al. 1996,
Broer et al. 1997]. Their method is a variation of the graph
transform that allows the computation
of a normally hyperbolic
invariant circle of saddle-type of a three-dimensional map.
The key idea is to start with a known invariant circle H of
a map f together with the Df-invariant splitting of the tangent
space at H. This splitting induces Df-invariant stable and
unstable normal bundles that are embedded in  in a neighborhood
of H. Because H is normally hyperbolic, these embedded normal
bundels form a well-defined coordinate system in a neighborhood of
H. The invariant circle
in a neighborhood
of H. Because H is normally hyperbolic, these embedded normal
bundels form a well-defined coordinate system in a neighborhood of
H. The invariant circle
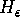 of a small perturbation
of a small perturbation 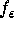 of f is
computed as the graph over the known circle H in the coordinate
system given by the embedded normal bundles. As a special feature of
the method
the new
of f is
computed as the graph over the known circle H in the coordinate
system given by the embedded normal bundles. As a special feature of
the method
the new 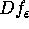 -invariant splitting of the invariant circle
-invariant splitting of the invariant circle 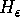 is computed in a second step,
regardless of the dynamics on
is computed in a second step,
regardless of the dynamics on
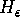 . Consequently, the method can be used in
a continuation setting: a known invariant circle can be
followed by increasing
. Consequently, the method can be used in
a continuation setting: a known invariant circle can be
followed by increasing 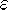 in small steps. The embedded unstable
normal bundle
in small steps. The embedded unstable
normal bundle 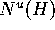 of
[Osinga 1996,
Broer et al. 1996,
Broer et al. 1997]
is the first order approximation of
of
[Osinga 1996,
Broer et al. 1996,
Broer et al. 1997]
is the first order approximation of 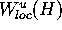 , the local
unstable manifold of H.
, the local
unstable manifold of H.
This allows us to globalize this first order approximation to
compute a significant piece of 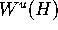 .
To be more concrete, the invariant
circle H is known in a
finite mesh M of points, and at each mesh
point
.
To be more concrete, the invariant
circle H is known in a
finite mesh M of points, and at each mesh
point 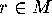 we are
given the normal direction
we are
given the normal direction 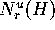 of the embedded normal bundle.
(Since
of the embedded normal bundle.
(Since  is of saddle-type,
is of saddle-type,
 is a vector.)
We now choose a linear foliation
is a vector.)
We now choose a linear foliation
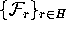 of the state space so that each
leaf has a
unique intersection with H.
From the unstable normal bundle
of the state space so that each
leaf has a
unique intersection with H.
From the unstable normal bundle 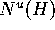 above
we compute
unit vectors
above
we compute
unit vectors 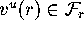 for all
for all 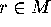 , such that
, such that 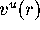 is tangent to
is tangent to 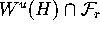 . Starting from the linear
approximation given by M and
. Starting from the linear
approximation given by M and 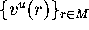 ,
we compute the
intersection of the unstable manifold
,
we compute the
intersection of the unstable manifold 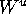 with the
finitely many leaves
of
with the
finitely many leaves
of 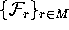 .
For this to work we need the following.
.
For this to work we need the following.
Foliation Condition
In each leaf of 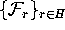 there is a
unique curve of intersection with the unstable manifold
there is a
unique curve of intersection with the unstable manifold
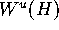 .
In other words, the unstable manifold intersects each leaf
.
In other words, the unstable manifold intersects each leaf
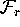 transversally.
transversally.
Assuming this foliation condition is satisfied,
we can compute
the unstable manifold in each of the leaves
of 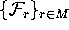 as
a sequence of points that have a prescribed distance
from each other.
The set of sequences in a finite number
of leaves defines a mesh
that represents the unstable manifold.
This computation can be done
in steps by adding rings or bands,
that is, by adding
a single new point to the sequence in
each leaf. In this way, one can see the
unstable manifold grow during the computation.
as
a sequence of points that have a prescribed distance
from each other.
The set of sequences in a finite number
of leaves defines a mesh
that represents the unstable manifold.
This computation can be done
in steps by adding rings or bands,
that is, by adding
a single new point to the sequence in
each leaf. In this way, one can see the
unstable manifold grow during the computation.
The linear foliation 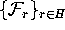 has no
dynamical property, but should be seen as an a priori
definition of the mesh. By
adding additional leaves during the computation we
guarantee the quality of the mesh on the unstable
manifold. By construction, our method is independent of
the dynamics on the invariant circle.
We can use it for the computation of the
two-dimensional unstable manifold of a fixed point, if we interpret
the fixed point as an invariant circle in polar coordinates.
A detailed description of the algorithm can be found in
Section 3.
has no
dynamical property, but should be seen as an a priori
definition of the mesh. By
adding additional leaves during the computation we
guarantee the quality of the mesh on the unstable
manifold. By construction, our method is independent of
the dynamics on the invariant circle.
We can use it for the computation of the
two-dimensional unstable manifold of a fixed point, if we interpret
the fixed point as an invariant circle in polar coordinates.
A detailed description of the algorithm can be found in
Section 3.
The procedure of adding rings or bands
fails when the computed portion of the unstable
manifold no longer intersects
each leaf of 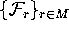 in a unique
curve. A piece of the intersection is then missed in
the computation, and the algorithm
is lacking information about a part of the unstable
manifold. Because this information is necessary in the
computation, the algorithm stops.
This is discussed in more detail in
Section 6; see also
Figure 6 and
Figure 18.
Note that by definition the
foliation
in a unique
curve. A piece of the intersection is then missed in
the computation, and the algorithm
is lacking information about a part of the unstable
manifold. Because this information is necessary in the
computation, the algorithm stops.
This is discussed in more detail in
Section 6; see also
Figure 6 and
Figure 18.
Note that by definition the
foliation 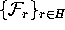 is transverse to
is transverse to 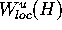 so that at least a part of
so that at least a part of 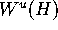 can be
computed. Furthermore, we think that many interesting
examples satisfy the foliation condition;
see Section 5. Possible relaxations
of the foliation condition are discussed in
Section 6.
can be
computed. Furthermore, we think that many interesting
examples satisfy the foliation condition;
see Section 5. Possible relaxations
of the foliation condition are discussed in
Section 6.
In summary, we present an algorithm that computes a
growing piece of the two-dimensional
unstable manifold of a
normally hyperbolic invariant circle of saddle-type or
a hyperbolic saddle point, until the unstable manifold
becomes tangent to the foliation 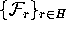 .
The mesh representing the invariant manifold is of a
prescribed quality. This allows us to study
the global dynamics of many interesting systems,
in particular those that satisfy the Foliation
Condition.
.
The mesh representing the invariant manifold is of a
prescribed quality. This allows us to study
the global dynamics of many interesting systems,
in particular those that satisfy the Foliation
Condition.
This paper is organized as follows. In Section 2 we give an overview over the literature on the calculation of global unstable manifolds. In Section 3 we give a detailed description of the algorithm, and Section 4 deals with its correctness. The performance of our method is demonstrated in Section 5 with a number of examples. The applicability of the algorithm and some open problems are discussed in Section 6.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Wed Jul 2 10:50:50 1997