![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and ContentsWe now give a brief overview of the literature on the calculation of global unstable manifolds of both vector fields and maps.
The computation of the one-dimensional unstable manifold of an equilibrium of a vector field is now standard procedure; see [Back et al. 1992]. Because each of its two branches is a single orbit, it can be found by integration once a single point on the branch is known. In the special case that there is a one-dimensional unstable manifold of a vector field of finite length in the form of a homoclinic or heteroclinic connection, one can use a boundary value approach to compute the entire (connecting) manifold; see [Beyn 1990, Friedman and Doedel 1991, Bai et al. 1993, Moore 1995].
There are several methods for the computation of the
one-dimensional unstable manifold of a
hyperbolic fixed point 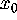 of the map f;
see for example [Simó 1989,
Parker and Chua 1989,
You et al. 1991,
Hobson 1993,
Homburg et al. 1996].
The idea is to first compute the local unstable manifold
of the map f;
see for example [Simó 1989,
Parker and Chua 1989,
You et al. 1991,
Hobson 1993,
Homburg et al. 1996].
The idea is to first compute the local unstable manifold 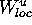 in a neighborhood U of
in a neighborhood U of 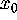 , either as a series representation
up to a given order [Simó 1989], or by means of the
graph transform [Osinga 1996,
Homburg et al. 1996]. In many cases already
the linear approximation
suffices; see
[You et al. 1991].
Then a fundamental domain in
, either as a series representation
up to a given order [Simó 1989], or by means of the
graph transform [Osinga 1996,
Homburg et al. 1996]. In many cases already
the linear approximation
suffices; see
[You et al. 1991].
Then a fundamental domain in
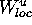 is iterated to obtain larger and larger pieces of
is iterated to obtain larger and larger pieces of
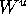 . Already in this approach one encounters
considerable difficulties, because one cannot iterate a fundamental domain
as a continuous object, but only as a discrete set of points.
. Already in this approach one encounters
considerable difficulties, because one cannot iterate a fundamental domain
as a continuous object, but only as a discrete set of points.
Typically the
fundamental domain becomes larger under iteration of f so that additional
points need to be added. Furthermore,
the unstable manifold may fold, and sharp turns
may be overlooked.
The solution is to add points when the distance
between consecutive points
becomes too large, or when the curvature of
the manifold becomes too big.
Points may be added in the original fundamental domain on 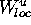 [Simó 1989,
You et al. 1991],
or in the previous iterate of the
fundamental domain
[Parker and Chua 1989,
Hobson 1993].
For reasons of efficiency it is
also useful to delete unnecessary points;
see [Parker and Chua 1989].
[Simó 1989,
You et al. 1991],
or in the previous iterate of the
fundamental domain
[Parker and Chua 1989,
Hobson 1993].
For reasons of efficiency it is
also useful to delete unnecessary points;
see [Parker and Chua 1989].
In the computation of a two-dimensional unstable manifold an additional problem arises: in general, points tend to accumulate on a one-dimensional submanifold under iteration of f, as is sketched in Figure 2. Therefore, it is not worthwhile to simply use the idea of iterating a fundamental domain as for the computation of one-dimensional unstable manifolds.
Most algorithms that compute two-dimensional unstable manifolds do so for vector fields. [Guckenheimer and Worfolk 1993] describes a method to compute the two-dimensional unstable manifold of the origin for the Lorenz system. The idea is to start with a small circle in the unstable eigenspace and to `push' it over the unstable manifold with the flow in the direction perpendicular to the old circle. By iterating this process one obtains a family of circles as an approximation of the unstable manifold. A similar idea that uses the normalized vector field is implemented by [Worfolk 1997]; see Figure 15. In [Friedman and Doedel 1991] the two-dimensional connecting manifold between two equilibria is computed by defining a suitable one-parameter family of boundary problems.
A special case for vector fields is a periodic orbit of
saddle-type. Orbits on its unstable manifold do not accumulate on a
one-dimensional submanifold. Hence, the unstable manifold can be
approximated by integrating a sufficient number of points on
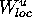 . This approach is used in
[Thurman and Worfolk 1996] and, in a refined version that uses
remeshing, in
[Taylor et al. 1989,
Johnson et al. 1995]. We note
that in this situation often the global dynamics is completely
understood from the computation of the
one-dimensional manifold of the corresponding
Poincaré map on a suitable section.
. This approach is used in
[Thurman and Worfolk 1996] and, in a refined version that uses
remeshing, in
[Taylor et al. 1989,
Johnson et al. 1995]. We note
that in this situation often the global dynamics is completely
understood from the computation of the
one-dimensional manifold of the corresponding
Poincaré map on a suitable section.
We now discuss methods for the computation of the two-dimensional unstable manifolds of maps. In [Tabacman 1993] an algorithm is described that generates a good approximation of the unstable manifold in a neighborhood of a saddle point; see Lomelí and Meiss 1997 for an application. The idea is to iterate a uniform mesh backwards by the linearized map, and then iterate the resulting mesh under the nonlinear map. [Dellnitz and Hohmann 1996] present the only algorithm, so far, for the computation of two- or higher-dimensional unstable manifolds of a map. Their idea is to find a covering of a local piece of the unstable manifold by small boxes with a subdivision algorithm. In a second step, a region of interest of the phase space is subdivided into small boxes, and it is decided which of these boxes are intersected by iterates of the previously computed boxes representing the local piece of the unstable manifold. In this way, a covering of the unstable manifold with objects of a larger dimension than the manifold itself (three-dimensional boxes in our setting) is obtained. This is quite different from our idea of globalizing the local unstable manifold as a two-dimensional object.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:48:24 1997