![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
We presented an algorithm for the computation
of the two-dimensional unstable manifold of
a normally hyperbolic invariant circle
or a hyperbolic fixed point of a three-dimensional
diffeomorphism. Its main feature is the use of a
linear foliation to assure the quality of the mesh
on the unstable manifold.
Because of normal hyperbolicity it is always possible to find
a linear foliation that is transverse to 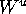 in a neighborhood of the invariant circle or fixed point.
If this foliation
is also transverse to all of
in a neighborhood of the invariant circle or fixed point.
If this foliation
is also transverse to all of 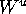 the Foliation
Condition is satisfied. This means that the
complete unique intersection curve in each leaf
can be computed.
If the Foliation Condition is not satisfied the algorithm
computes
the Foliation
Condition is satisfied. This means that the
complete unique intersection curve in each leaf
can be computed.
If the Foliation Condition is not satisfied the algorithm
computes 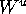 until an extra branch in one of the leaves
is missed. In any case, a first piece of the unstable manifold
is caclulated that contains
until an extra branch in one of the leaves
is missed. In any case, a first piece of the unstable manifold
is caclulated that contains 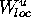 .
.
To find the intersection curve of 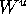 with a leaf we compute a sequence of points by
taking
with a leaf we compute a sequence of points by
taking  -steps along this curve.
We remark that this idea can also be used
to globalize the one-dimensional unstable manifold of a hyperbolic
fixed point as a curve. The only difference is that the inverse image
of a new point along the unstable manifold
lies in the already computed piece of the curve (and not in
a different leaf).
-steps along this curve.
We remark that this idea can also be used
to globalize the one-dimensional unstable manifold of a hyperbolic
fixed point as a curve. The only difference is that the inverse image
of a new point along the unstable manifold
lies in the already computed piece of the curve (and not in
a different leaf).
The Foliation Condition is in fact a condition on the global
nature of 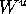 : the unstable manifold may fold, but not
in such a way that
it becomes tangent to a suitable linear foliation;
see Figure 18.
Although we found several interesting examples of
unstable manifolds
that satisfy the Foliation Condition, this
condition restricts the class of maps for which
our algorithm can be used; see Section 5.4.
The algorithm presented here
should be considered
as a first step.
A promising idea for a general algorithm, using the fact
that
: the unstable manifold may fold, but not
in such a way that
it becomes tangent to a suitable linear foliation;
see Figure 18.
Although we found several interesting examples of
unstable manifolds
that satisfy the Foliation Condition, this
condition restricts the class of maps for which
our algorithm can be used; see Section 5.4.
The algorithm presented here
should be considered
as a first step.
A promising idea for a general algorithm, using the fact
that 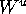 is an immersed manifold, is
the following. It is crucial that
in each leaf there is a unique branch of the intersection curve of
is an immersed manifold, is
the following. It is crucial that
in each leaf there is a unique branch of the intersection curve of
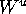 in a
in a  -neighorhood of the farthest point.
This is a local condition that is satisfied if we
impose the Foliation Condition. In the future we plan to work with
a local moving foliation that changes at each step and is
perpendicular to the circle added last.
-neighorhood of the farthest point.
This is a local condition that is satisfied if we
impose the Foliation Condition. In the future we plan to work with
a local moving foliation that changes at each step and is
perpendicular to the circle added last.
It is possible to adjust the algorithm so that it can be used to compute two-dimensional unstable manifolds in systems of dimension higher than three. The computation of unstable manifolds of dimension higher than two is much more complicated, and also requires the solution of serious problems concerning data management and visualization.
In the immediate future we intend to allow for
steps of different sizes
in different leaves. This is necessary in the
special case that the unstable manifold is bounded.
Consider a two-dimensional bounded unstable manifold
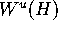 of a normally hyperbolic invariant
circle H that converges to an attracting invariant
circle. The present algorithm computes a growing ring
of
of a normally hyperbolic invariant
circle H that converges to an attracting invariant
circle. The present algorithm computes a growing ring
of 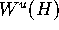 with the same arclength distance from H
in each leaf. The algorithm stops when the attractor is reached in
one leaf, which means that,
in general, a piece of the compact manifold
with the same arclength distance from H
in each leaf. The algorithm stops when the attractor is reached in
one leaf, which means that,
in general, a piece of the compact manifold
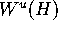 is missed. The solution is to monitor
the distance from the attractor in each leaf, and to adjust the
step-size along the intersection curve with
is missed. The solution is to monitor
the distance from the attractor in each leaf, and to adjust the
step-size along the intersection curve with 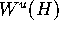 accordingly.
accordingly.
All algorithms that compute a two-dimensional unstable manifold, with
the exception of [Dellnitz and Hohmann 1996], are for
vector fields; we refer to
[Guckenheimer and Worfolk 1993,
Worfolk 1997,
Johnson et al. 1995].
A vector field can be seen as a one-parameter family of time t
maps. It is possible to use our algorithm for finding
a two-dimensional unstable manifold of a vector field
by considering the time 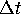 map for a fixed
map for a fixed 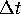 . However,
the algorithms for vector fields are better suited for this
task; see also Section 5.4. Note that
for a vector field, information about tangents is available
that can be used to move in a
prescribed direction. Furthermore, the integration time
may be varied during the computation.
Both is not possible for a single, fixed time
. However,
the algorithms for vector fields are better suited for this
task; see also Section 5.4. Note that
for a vector field, information about tangents is available
that can be used to move in a
prescribed direction. Furthermore, the integration time
may be varied during the computation.
Both is not possible for a single, fixed time 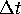 map.
The strength of our algorithm for the study
of vector fields lies in considering Poincaré maps.
As was demonstrated in Section 5.5,
it allows to compute the three-dimensional unstable
manifold of a periodic orbit or
an invariant torus of a four-dimensional vector
field.
map.
The strength of our algorithm for the study
of vector fields lies in considering Poincaré maps.
As was demonstrated in Section 5.5,
it allows to compute the three-dimensional unstable
manifold of a periodic orbit or
an invariant torus of a four-dimensional vector
field.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:55:55 1997