Next: Summer Enrichment
Up: Of Museums and Icosahedra
Prev: Museum Mathematics
Mathematics on the Internet
Every year, millions of people go to science museums. We are rapidly
approaching an age in which a comparable number of people have access
to the Internet. The past year has seen a tremendous surge in the
number of Internet users; a partial explanation for this is the
popularity of so-called World-Wide Web (WWW) browsers such as NCSA
Mosaic. (See the August 1994 FOCUS for more information on
using NCSA Mosaic as a tool for Internet access.) You might say that
the Internet has become a ``Web of Dreams'' that operates under the
philosophy ``Build it, they will come.'' Using a WWW browser, it is
relatively painless (in fact, it's a lot of fun!) to electronically
obtain information from all over the world. The WWW browsers use
``hyperlinks'' to allow the user to pass from one site of information
to another without having to worry (or even know!) about where the
information is coming from.
We at the Geometry Center are using the Web as part of our effort to
make mathematics more accessible and understandable to
non-mathematicians. Documents are written in hypertext, which allows
users to ``click'' on certain words, phrases, and pictures in order to obtain
additional information. Our hypertext documents are designed to
present mathematics to the masses using a combination of expository
prose, computer-generated graphics, and animations. Furthermore, we
have used the unique capabilities of the Web to produce interactive
documents that allow users to explore and discover mathematics for
themselves. We have a very popular Gallery of of Interactive On-Line
Geometry in which Internet explorers investigate and visualize the
mathematics of quasiperiodic tilings of the plane, wallpaper groups,
geodesics on manifolds, Riemann surfaces, and symmetries of the
hyperbolic plane. The Geometry Center's WWW documents are accessible from
our so-called
``home page.''
In fact, this article is
available on-line as well as part of the
Geometry Center's Online Multimedia Document Library!
The Geometry Center is also looking at how to use the World-Wide Web
in order to disseminate research-level mathematics to professional
mathematicians. Already we live in an age in which a large portion of
research mathematics is distributed in preprint form, thanks to
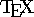 for formatting equations, electronic drawing programs for producing
figures, and laser printers for putting it all on paper. Color
printers and copiers now allow mathematicians to include color figures
in preprints, thus increasing our ability to convey information about
geometric structures. Yet our preprints and journal articles are
fundamentally limited to static images. No paper-based preprint or
journal allows authors to publish an animation showing a rotating
surface. None allow the reader to interactively alter parameters in a
model and to subsequently generate a new figure that perhaps
even the author has never seen. However, these abilities are available
in hypertext documents, and the Geometry Center has begun to
experiment with these possibilities through its Web documents.
for formatting equations, electronic drawing programs for producing
figures, and laser printers for putting it all on paper. Color
printers and copiers now allow mathematicians to include color figures
in preprints, thus increasing our ability to convey information about
geometric structures. Yet our preprints and journal articles are
fundamentally limited to static images. No paper-based preprint or
journal allows authors to publish an animation showing a rotating
surface. None allow the reader to interactively alter parameters in a
model and to subsequently generate a new figure that perhaps
even the author has never seen. However, these abilities are available
in hypertext documents, and the Geometry Center has begun to
experiment with these possibilities through its Web documents.
As an example, we highlight a recent mathematical result by Center
postdoc
Davide Cervone.
Cervone discovered a certain immersion of the
real projective plane with one handle into three-space that settles a
long-standing conjecture in simplicial geometry. The result is being
submitted to a traditional journal, but because the fundamental result
concerns exhibiting a surface with special properties, Cervone chose
to write a preprint using hypertext
as his medium.
Cervone's document
begins with a highly
accessible introduction to the problem (complete with hyperlinks to
basic definitions!), and then proceeds to present and prove his new
result. He then provides the reader with multiple ways of visualizing
and interacting with this new immersion; there are movies of the
rotating surface and of a family of level sets, and there are
interactive pictures that the reader may manipulate in order to see
the surface from a desired viewpoint. We are currently considering
how to use this powerful medium to communicate mathematics in
curricular material for undergraduates in mathematics, science, and
engineering.
We believe that our presentation of mathematics on the Web is
successfully reaching thousands of people from all walks of life, but
it is very difficult to quantitatively assess the impact of our efforts.
We have records of hundreds of thousands of
connections to the Geometry Center WWW documents, but we cannot
evaluate who these people are, nor determine their backgrounds. Are we
reaching teachers from high schools and community colleges? Are we
reaching populations that are underrepresented in mathematics? Are we
making a difference in the way that ordinary people think about
mathematics? Are we affecting the way that mathematicians think about
presenting mathematics? We have some (very
positive) comments sent to us by users, but it is difficult to
extrapolate from this data. We need to understand how to
better assess our outreach through the Internet.
Next: Summer Enrichment
Up: Of Museums and Icosahedra
Prev: Museum Mathematics
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Frederick J. Wicklin <fjw@geom.umn.edu>
Comments to:
webmaster@www.geom.uiuc.edu
Created: September 26, 1994 ---
Last modified: Jul 21 1996
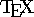 for formatting equations, electronic drawing programs for producing
figures, and laser printers for putting it all on paper. Color
printers and copiers now allow mathematicians to include color figures
in preprints, thus increasing our ability to convey information about
geometric structures. Yet our preprints and journal articles are
fundamentally limited to static images. No paper-based preprint or
journal allows authors to publish an animation showing a rotating
surface. None allow the reader to interactively alter parameters in a
model and to subsequently generate a new figure that perhaps
even the author has never seen. However, these abilities are available
in hypertext documents, and the Geometry Center has begun to
experiment with these possibilities through its Web documents.
for formatting equations, electronic drawing programs for producing
figures, and laser printers for putting it all on paper. Color
printers and copiers now allow mathematicians to include color figures
in preprints, thus increasing our ability to convey information about
geometric structures. Yet our preprints and journal articles are
fundamentally limited to static images. No paper-based preprint or
journal allows authors to publish an animation showing a rotating
surface. None allow the reader to interactively alter parameters in a
model and to subsequently generate a new figure that perhaps
even the author has never seen. However, these abilities are available
in hypertext documents, and the Geometry Center has begun to
experiment with these possibilities through its Web documents.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page