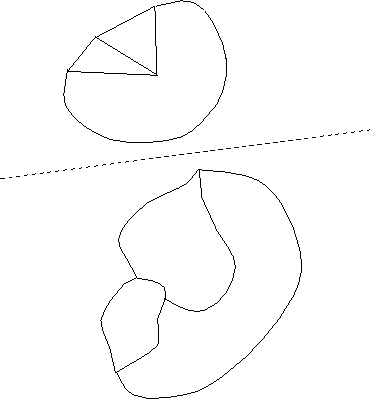
Figure 2: These two maps are considered the same (topologically equivalent), because it is possible to continuously move one to obtain the other.
A map in the plane is a collection of vertices and edges (possibly curved) joining the vertices such that if you cut along the edges the plane falls apart into polygons. These polygons are called the faces. A map on the sphere or any other surface is defined similarly. Two maps are considered to be the same if you can get from one to the other by a continouous motion of the whole plane. Thus the two maps in figure 2 are considered to be the same.
Figure 2: These two maps are considered
the same (topologically equivalent), because it is possible
to continuously move one to obtain the other.
A map on the sphere can be represented by a map in the plane by removing a point from the sphere and then stretching the rest of the sphere out to cover the plane. (Imagine popping a balloon and stretching the rubber out onto on the plane, making sure to stretch the material near the puncture all the way out to infinity.)
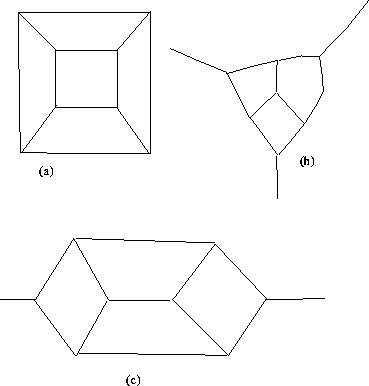
Figure 3: These three diagrams are maps
of the cube, stretched out in the plane. In (a), a point has been
removed from a face in order to stretch it out. In (b), a vertex has
been removed. In (c), a point has been removed from an edge.
Depending on which point you remove from the sphere, you can get different maps in the plane. For instance, figure 3 shows three ways of representing the map depicting the edges and vertices of the cube in the plane; these three different pictures arise according to whether the point you remove lies in the middle of a face, lies on an edge, or coincides with one of the vertices of the cube.
For the regular polyhedra,
the Euler number 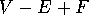 takes on the value 2,
where
takes on the value 2,
where 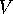 is the number of vertices,
is the number of vertices, 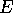 is the number of edges,
and
is the number of edges,
and 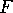 is the number of faces.
is the number of faces.
The Euler number (pronounced `oiler number')
is also called the Euler characteristic,
and it is commonly denoted by the Greek letter 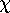 (pronounced `kai',
to rhyme with `sky'):
(pronounced `kai',
to rhyme with `sky'):

This exercise is designed to investigate the extent to which it is true that the Euler number of a polyhedron is always equal to 2. We also want you to gain some experience with representing polyhedra in the plane using maps, and with drawing dual maps.
We will be distributing examples of different polyhedra.
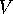 ,
, 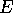 ,
, 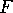 , and the Euler number
, and the Euler number 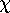 .
.
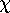 is frequently very small compared with
is frequently very small compared with 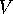 ,
, 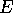 , and
, and 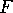 ,
Can you think of ways to find the value of
,
Can you think of ways to find the value of 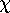 without
having to compute
without
having to compute 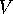 ,
, 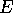 , and
, and 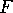 , by
`cancelling out' vertices or faces
with edges?
This gives another way to check your work.
, by
`cancelling out' vertices or faces
with edges?
This gives another way to check your work.
The dual of a map is a map you get by putting a vertex in the each face, connecting the neighboring faces by new edges which cross the old edges, and removing all the old vertices and edges. To the extent feasible, draw a map in the plane of the polyhedron, draw (in a different color) the dual map, and draw a net for the polyhedron as well.