Notation for some knots
Next: Knots diagrams and
Up: Geometry and the Imagination
Previous: Maps
It is a hard mathematical question to completely codify
all possible knots. Given two knots, it is hard to tell whether
they are the same. It is harder still to tell for sure
that they are different.
Many simple knots can be arranged in a certain form, as illustrated
below, which is described by a string of positive integers along
with a sign.
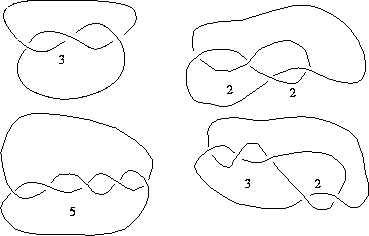
Figure 4: Here are drawings of
some examples of knots that Conway `names' by a string of positive integers.
The drawings use the convention that when one strand crosses under
another strand, it is broken.
Notice that as you
run along the knot, the strand alternates going over and under at
its crossings. Knots with this property are called alternating
knots. Can you find any examples of knots with more than one
name of this type?
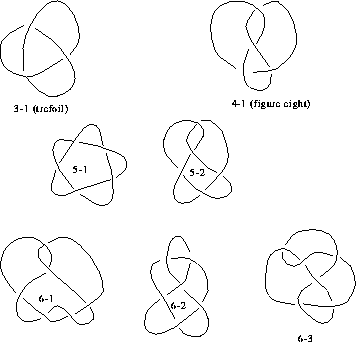
Figure 5: Here are the knots with
up to six crossings. The names follow an old system, used widely
in knot tables, where the 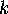 th knot with
th knot with  crossings is called
crossings is called
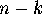 .
Mirror images are not included: some of these
knots are equivalent to their mirror images, and some are not.
Can you tell which are which?
.
Mirror images are not included: some of these
knots are equivalent to their mirror images, and some are not.
Can you tell which are which?
Next: Knots diagrams and
Up: Geometry and the Imagination
Previous: Maps
Peter Doyle

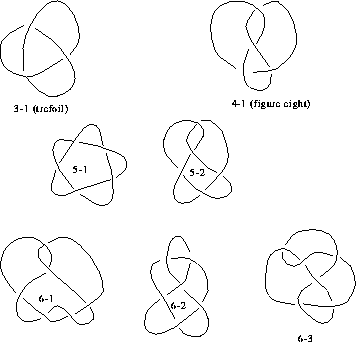
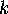 th knot with
th knot with  crossings is called
crossings is called
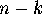 .
Mirror images are not included: some of these
knots are equivalent to their mirror images, and some are not.
Can you tell which are which?
.
Mirror images are not included: some of these
knots are equivalent to their mirror images, and some are not.
Can you tell which are which?